以有效卫星数为4颗为例，分别使用ILS、EKF和改进的EKF算法进行定位，得到以ECEF坐标系下XYZ三维坐标表示的定位结果，如图1所示。

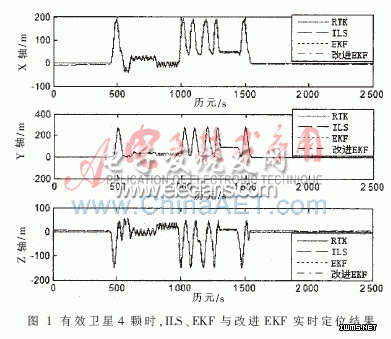
　　由图 1可知，接收机在前400 s时基本保持静止，然后开始运动至1 600 s，最后逐步静止至测试结束。三种解算方法都可以较好地进行定位解算。为了更好地分析定位结果，画出图 1中的XYZ三维坐标上的定位误差的均方根，如图 2所示。

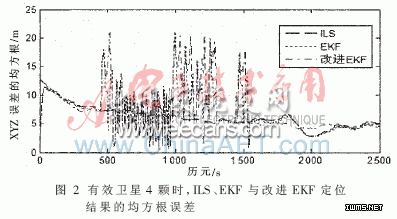
　　为了更好地比较ILS、普通EKF与改进EKF算法，计算图 2中三种算法在XYZ三个坐标方向上的定位结果的均方根误差的平均值，如表1所示。

　　从图2和表1可以更清晰地看出，在有效卫星不少于4颗时，三种算法在以ECEF坐标系表示的XYZ方向上的定位误差的均方根均不超过20 m，平均定位误差不超过10 m，定位解算精度都很好。其中改进的EKF与普通EKF定位精度相当，而ILS的定位均方根误差抖动很小。这是因为，每当有新的测量数据时，ILS算法都会经过多次迭代计算直至结果收敛，而EKF与改进的EKF算法均只是利用新息进行一次计算，计算量要远远小于ILS，故而定位结果会稍有抖动。

　　3.2 有效卫星数只有3颗时的定位结果

　　在有效卫星数只有3颗时，ILS无法进行定位。分别使用普通EKF和改进的EKF算法进行定位，得到在ECEF坐标系下的XYZ三维坐标上的定位结果，如图 3所示。

　　为了更好地分析定位结果，画出图 3中的XYZ三维坐标上的定位误差的均方根，如图 4所示。

　　为了更好地比较普通EKF算法与改进EKF算法，计算图 3中两种算法XYZ三维坐标上的定位结果的均方根误差的平均值，如表 2所示。

　　由图 3、图 4和表 2可知，在只有3颗有效卫星的情况下，普通EKF的定位结果会出现明显的偏移，而本文提出的改进的EKF算法的定位结果与参考轨迹拟合得很好，各个方向上的平均定位误差均不超过10 m，定位精度很好。这说明本文提出的改进EKF算法在只有3颗有效卫星时，极大地提高了EKF的定位精度。与理论结果吻合。

　　3.3 有效卫星为3颗时改进EKF与有效卫星为4颗时普通EKF 的定位结果

　　为了进一步分析改进EKF算法的性能，将改进EKF算法在只有3颗有效卫星时的定位误差与普通EKF算法在有4颗有效卫星时的定位误差进行比较，如图 5所示。

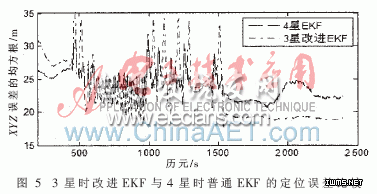
　　计算图 5中的两种情况下XYZ三维坐标上的平均误差的均方根，如表3所示。

　　由图 5和表 3可知，在只有3颗有效卫星时，本文提出的改进EKF算法所增加的先验信息与增加一颗卫星的测量信息的效果基本一致。故而说明在出现GPS信号阻塞的情况下，只有3颗有效卫星时，此改进EKF算法的定位解算精度非常好。

　　综上所述，利用实测的卫星数据进行验证，结果表明：在3颗有效卫星的情况下，在静止状态和车载状态下，改进的EKF算法的定位精度均明显优于普通的EKF，且与4颗有效卫星时EKF的定位精度相当;在不少于4颗有效卫星的情况下，在静止状态和车载状态下，改进EKF算法的定位精度与普通EKF相当。由此说明，本文提出增加的先验信息在已有足够测量信息时，并不会影响定位精度，而只有在3颗有效卫星时，测量信息对于定位精度的改进与一颗有效卫星的测量信息效果基本一致，从而大大提高了EKF算法的鲁棒性。

　　总结

　　针对这一问题提出了一种改进的EKF算法。该算法利用在垂直地面方向上的位置变化缓慢这一运动特性，建立了改进EKF算法的系统模型。通过理论分析得到了滤波器参数，最后利用真实的GPS卫星数据进行验证。实验结果表明，在可见卫星数不少于4颗时，此改进的EKF算法定位精度与普通的EKF算法基本相同;在GPS信号阻塞只有3颗可见卫星时，此改进的EKF算法的定位精度明显优于普通的EKF算法。本文提出的改进EKF算法适合车载等地面运用，不适合在垂直地面方向上高速运动的情形。

上一页  [1] [2] [3]