·上一文章:CDMA 2000系统中前向链路卷积编码器的FPGA实现
·下一文章:无线传感器网络3G网关的设计与研制
双天线系统是一个无源二端口网络,用ai表示第i个端口的入射波,用bi表示第i个端口的反射波。入射波矢量a=(a1,a2)T,反射波矢量b=(b1,b2)T,其中:T表示矩阵的转置。则有:
![]()
所有的波矢量都是复数,则入射功率和反射功率由下式给出:
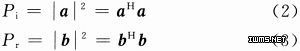
式中:|·|表示复数的模,上角标H表示厄米特转置。那么,辐射功率就可以表示为:
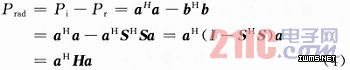
式中:H就是辐射矩阵,并且辐射矩阵是个厄米特量(HH=H),而厄米特矩阵是可以通过一个相似变换而对角化的。因此有:
![]()
式中:A=diag{λ1,λ2},而Q是幺正的(即QQH=I)。根据厄米特矩阵的性质,两个正交值λ1和λ2都是实数,并且小于等于1。将式(5)代入式(4)得:
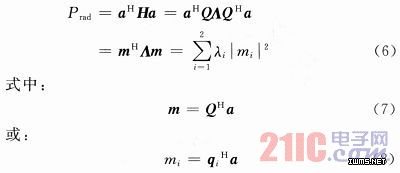
则Q矩阵的第i列qi就称为天线阵列的正交模式。|ai|2表示第i个端口的入射功率;|mi|2表示第i个正交模式的激发功率。由于Q的幺正性,有|a|2=|m|2,这就保证了入射总功率等于激发起的正交模总功率。而λi则反应了正交模式的辐射效率。
与辐射功率相对的是反射功率。根据(5)式及厄米特矩阵的性质,如果Q可以将H化为对角矩阵,则S也可以化为对角矩阵。有:
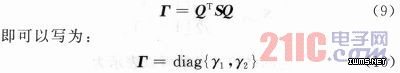
则反射矢量可以写为:
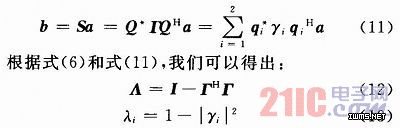
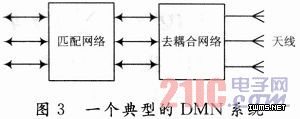
为了使正交模式的辐射效率最大,文献和文献详细论述了等效耦合参数的方法。对于一个双天线系统,等效去耦合网络如图4所示,其中S是天线的反射参数,SD是去耦合网络的反射参数,文献指出加入了去耦合系统的S参数可以表示为: