在同一系统中，采用同样的方法针对最陡下降法和LMS算法进行仿真，并与分段变步长算法的仿真结果进行比较，得到频谱图如图4所示。

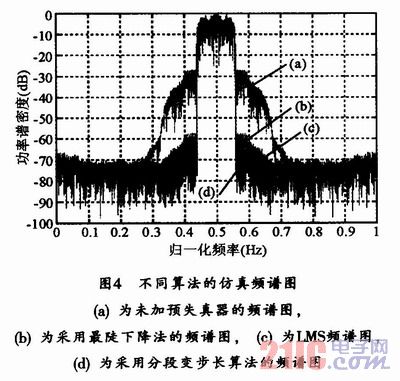
3．2 性能比较
    采用归一化均方误差(NMSE)来表征计算的收敛速度和计算精度，其表达式为
   
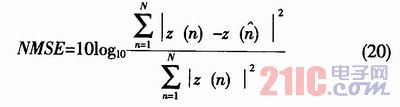
    每迭代一次，按上式求出NMSE的值并记录，三种自适应算法得到的仿真结果如图5所示，分段变步长算法的迭代次数明显少于最陡下降法及LMS算法。

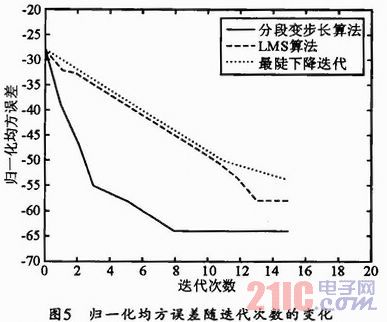
    采用误差矢量幅度(EVM表征带内失真，相邻信道功率比ACPR表征带外失真。
   
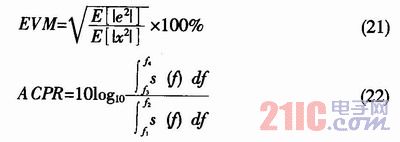
    其中，s(f)为功率谱密度， [f1，f2]为传输信道，[f3，f4]为相邻信道。
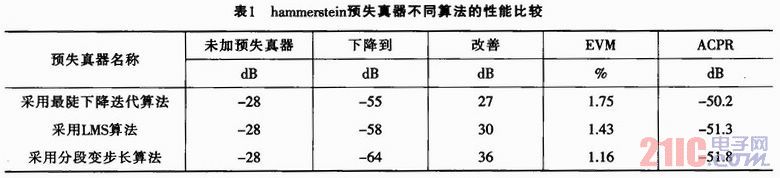
    按照(21)与(22)两式分别计算最陡下降法、LMS算法及分段变步长算法，得到结果如表1所列。

4 结束语
    本文采用Wiener模型作为功率放大器，与之相逆的hammerstein模型作为预失真器，用间接学习的预失真方法，采用三种不同的自适应算法最陡下降法、LMS算法、分段变步长算法进行系统仿真比较，通过matlab仿真结果表明，分段变步长自适应算法不仅在收敛速度(迭代次数)上明显优于其他两种自适应算法，并在带内失真与带外失真较之其他两种算法也有明显改善。

上一页  [1] [2] [3]