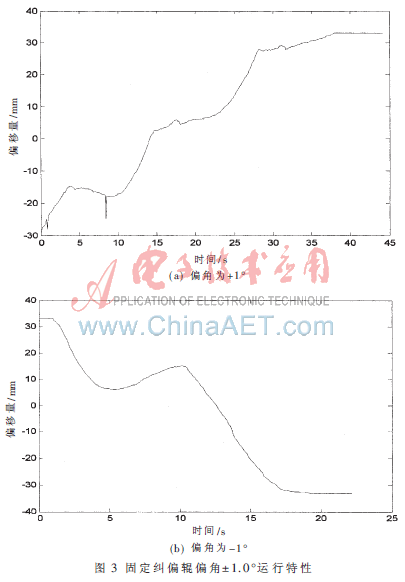
图4为增大角度分别至±1.5°时，薄带中心线的两个运动轨迹，可以看出，其横向移动速度比摆角为1°时明显加快。

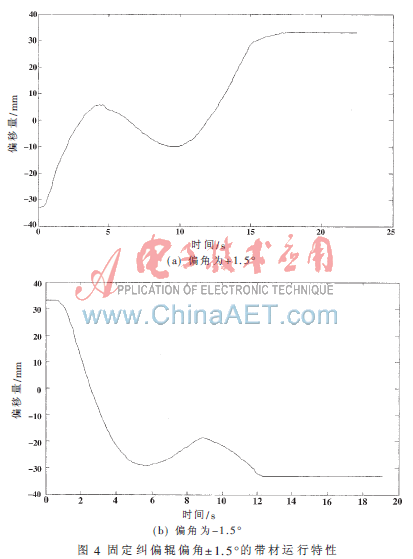
    测试结果说明，薄带能够在摆角作用下，受控于纠偏辊沿横向产生期望运动，且随摆角的增大而偏移速度加大。
4.2 纠偏控制实验
    根据实际测试结果获得的各项参数，分别设计了两种基于数字控制纠偏算法： (1)在薄带偏移时输出固定偏角(分别试验了摆角0.5°、1°、1.5°)，每次保持时间1 s；(2)设置摆角为薄带偏移量的函数,随偏移量大小而相应变化。
    图5为在第一种控制算法作用下带材中心线轨迹。可以看出，带材已经完全受控，可以在机构上稳定运行。图中曲线上较大尖刺为人为反复遮挡CCD探头模拟产生扰动，薄带的自动恢复过程。虽然薄带可以稳定运行，但是波动较大，稳定精度不高。带材运行速度不能过高。

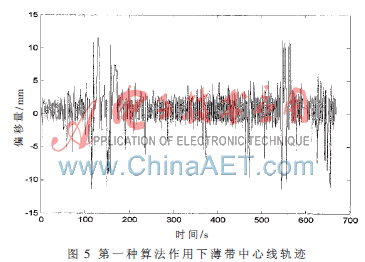
    图6为利用第二种算法后带材中心线轨迹，其中的几处较大尖刺同样为人为反复遮挡CCD探头，模拟扰动，薄带的自动恢复过程。而小幅度周期波动为带材闭合接头边缘不整齐产生的波动。不计上述扰动误差，可以实现的控制精度达到±1 mm，薄带运行速度可以进一步加快，直至实验设备所能达到的最高运行速度。

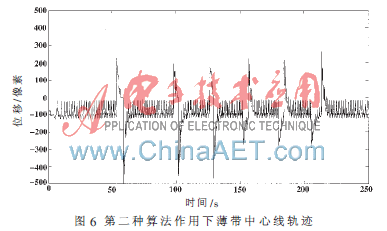
　　本文完成了数字控制系统的设计制造及调试，进一步开展针对其功能及性能要求的开环测试，定量地明确了电磁纠偏辊的输入位移与输出摆角之间的关系，以及摆角与薄带中心线影响关系。经过不断尝试改进，最终实现了电磁纠偏辊对薄带运行的稳定控制。带材运行平稳，控制动态误差小，最高运行速度400 m/min(当时实验设备能够实现的最高速度)。
参考文献
[1] 唐英.带钢跑偏控制[J].重型机械科技，2007(3)：4-6，11.
[2] 欧阳克诚，方胜年.转向单辊纠偏装置纠偏效果分析[J].重型机械，2000(2).
[3] 刘强，杨福兴，赵雷.新型纠偏方式—电磁纠偏的分析与设计[J].无线电工程，2007,10(17):42-43.
[4] 况群意.硅钢机组张力辊打滑现象分析和解决措施[J].机械设计与制造，2007(11):108-109.
[5] 赵启林,刘相华,王国栋.基于BP神经网络的带钢冷轧摩擦模型[J].轧钢，2003,20(6):7-9.
[6] 聂松林，高和生，胡友民,等.机、液型带钢跑偏控制装置的设计[J].武汉冶金科技大学学报，1997,20(2).
[7] 周旭东，刘香茹，王国栋，等.热连轧机组带钢厚度与轧制力的变刚度法智能纠偏系统[J].钢铁，2003,38(5):40-43.
[8] 尹凌冰.大间隙磁力轴承非线性控制方法研究[D].北京：清华大学，2007.

上一页  [1] [2]