很显然,考虑交叉灵敏度的非线性方程(7)与线性近似的方程(8)相比,求得的应变和温度与实际值较为接近;但当被测量变化较小时,由式(8)可获得足够精确的解,且用线性方程近似求解可充分利用较为成熟的线性方程组的数值方法理沦,使问题大大简化,因此式(8)在实际应用中仍具有重要意义,而参量变化较大时,忽略交叉灵敏度对于求解精度影响较大。
2 交叉灵敏度分析
由交叉灵敏度公式S&epSILon;T=USα可知:
交叉灵敏度既与传感器应变片自身的压阻系数、弹性模量、温度系数有关,又与电桥的供电电压有关,因此应变和温度同时作用于传感器时,传感器的输出不是应变和温度单独作用时产生的输出量的简单迭加,还存在着热力学和力学量的相互作用,这个作用反映为交叉灵敏度,其大小反映了这种相互作用的程度。
实际上,交叉灵敏度反映了在不同应变时,温度灵敏度不是一个常数,而是随着应变的变化而变化,交叉灵敏度的大小描述了温度灵敏度偏离常数的程度。实验中通过在不同应变下测量温度灵敏度,作出ST-ε曲线,该曲线的斜率便反映了交叉灵敏度的大小。
3 计算实例
以IC Sensors公司的S17-30A型传感器为例,结合A/D转换器AD7731把模拟量转换成数字量—6位16进制原码,再把16进制的原码送入AT89c52单片机,由单片机送出原码值。实验中以标准压力作为输入,测取不同温度条件下16进制的原码值,实验数据如表1所示。
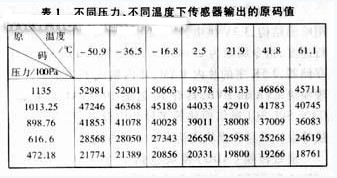
由表1中的数据,利用方程(7)进行计算。首先在同一温度不同压力条件下,然后再在同一压力不同温度条件下借助MATLAB语言分别解矩阵得:
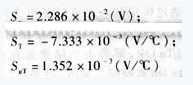
Sε,ST计算结果与传感器自身的技术指标非常接近,而交叉灵敏度SεT的技术指标只能通过上述方法或类似方法求出。
4 结论
利用上述方法借助方程(8)求出Sε,ST,通过对比可知,忽略交叉灵敏度将会带来很大的误差,该方法同样适用于其他半导体传感器。
参考文献
[1]余瑞芬.传感器原理[M].北京:航空工业出版社,1995.
[2]聂铁军.数值计算方法[M].西安:西北工业大学出版社,1990