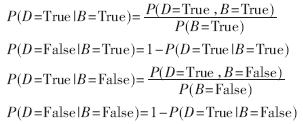节点的状态表示学生对该知识项的掌握程度,例如可以用4个等级来表示学生对知识项的掌握程度,A:表示学生对特定知识项已完全熟练掌握; B:表示学生对知识项基本掌握,但是仍有一些问题;C:表示学生处在初级阶段,有许多问题;D:表示学生对该知识项完全不了解。每一等级对应一个条件概率值(值的加权和为1),该值是基于对用户的观测值得到的用户对知识项的掌握程度。在系统设计过程中,为了简化,设置节点的状态为True(掌握)、False(未掌握)。
2.2.2 条件概率估计 经过上面的分析,接下来将讨论如何获得知识项之间的影响程度的条件概率表。
在贝叶斯网络构建中所有节点都要给定条件概率,对于没有父节点的节点,需要给定其先验概率,条件概率可以通过样本学习和通过专家估计获得[4]。
(1)设计分析
在由数据类型(A)、关系运算符(B)、变量(C)、While循环(D)教学资源构成的网络拓扑结构中,每个节点有两个离散的状态:True和False,如果需要,节点也可以包括更多的状态。设计网络时,必须指定每个节点的条件概率表,需要获得P(A)、P(C)、P(B)、P(D/C)、P(D/B)。
(2)样本收集
经验数据来自于某校某班学生学习“基本程序控制结构”这一章节后,经过测试,对其测试结果进行分析并获得学习知识项之间的相互影响程度,这样就确定了利用贝叶斯网络所建学生模型中网络拓扑知识项之间的条件概率函数。
将学生的得分情况分为100~90、90~80、80~70、70~60、60以下5个分数段。认为如果学生答对涉及到该知识项的题目,那么他对该知识项的知识状态为True(掌握);反之,如果答错,则认为他对该知识项的知识状态为False(未掌握)。
(3)学习条件概率表[5-6]
算法的设计思想是:首先按照网络构建中节点的拓扑顺序,根据每个分数段随机抽取n份考试的试卷用于对网络中各节点的状态进行赋值,当所有节点都被赋值一遍后就得到该网络中的一次采样样本,依此重复,得到10 n个样本,即一个样本序列;然后对该样本序列按相关列进行联合统计可得到网络近似推理结果。由于随机采样时考虑了节点的先验信息,所以当样本数n取很大时,这些采样样本的边缘统计量和条件统计量就可以趋近于事件的真实发生概率和条件发生概率。
对所有节点都采样了m遍,得到m组样本,即样本序列S,然后对样本序列S按列进行单独统计,得到节点的全概率;对多列进行联合统计,得到节点间的联合概率和条件概率。
所谓联合统计,就是把证据节点和推理目标节点的采样样本联合起来进行统计,就得到了给定证据后目标节点发生的条件概率和联合概率。对网络中的所有节点按拓扑顺序采样m次,得到样本序列S,对样本序列进行适当的统计,可以得到网络的近似推理结果。
节点Ni(i=1,…,n)发生的全概率就是单独对该列进行统计的结果。例如,要知道学生对于“变量”(C)已经True的情况的概率P(C=True),只要把对是T的那些样本挑选出来,然后统计一下T的个数,除以总的采样次数m,就可以近似为C这一知识项学生已经True(掌握)的概率,即:

节点Ni(i=1,…,n)发生的条件概率就是把那些条件节点和该节点所在的相关列联合起来进行统计。例如,计算节点“D”在节点“B”已经True(掌握)情况下发生T状态(D也为True)的概率,也即求P(D=True|B=True),可以这样进行:首先,把在“B”中是T的那些样本挑选出来,形成新的样本序列So,其组数为no;其次,把样本序列So中在“D”中是T的那些样本挑选出来,然后统计T的个数,除以no,就可以近似为“D”在“B”取状态为True的情况下发生False状态的概率:
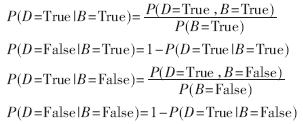
类似地,几个节点的联合概率则是把同时满足这些节点状态的样本挑出来,得到的样本组数除以总的样本组数m即可。
单独的节点状态概率,可以使用条件概率规则,并沿着边进行传播。
网络设计完成后,条件概率表进行了指定,网络进行了传播。
通过上面的分析,从定性方面完成了学生所学知识项的逻辑关系,并且通过经验数据获得了关于这些知识项之间存在影响程度的定量数据,最终构建成的个性化教学中关于《Delphi程序设计教程》课程中章节知识项的学生模型的框架如图1所示。
上一页 [1] [2] [3]