摘要：本文针对目前国内停车场普遍存在的停车难、管理乱等现实问题，提出了基于贝叶斯网络的停车场车位引导模型。通过选取停车行为相关因素作为选择变量，构建了面向停车引导的贝叶斯网络结构，并计算停车入位行为的最大后验概率，以此分析出停车引导的最佳路径。

    0 引言
    随着经济的持续快速发展，汽车消费进人了高速增长期，机动车保有量的增大不仅给城市道路交通带来了巨大的压力，同时停车设施短缺、停车难、管理乱等问题已成为影响城市交通发展的一大难题。停车场智能化车位引导算法可以有效引导待停车量，在不扩张停车场容量的前提下提高它的利用率。同时增强停车场的安全性和可靠性，节约大量的人力物力，具有十分重要的现实意义。
    1 贝叶斯网络简介
    贝叶斯网络（ BayesianNetwork、 BN）是人工智能领域的一种重要的处理概率问题的建模方法。＿贝叶斯网络是不确定性推理的图模型。在图模型中，节点表示变量，弧表示变量之间的依赖关系。
    贝叶斯网络推理是统计模型推理的一种基本方法，其基本思想是：已知条件概率表达式和先验概率分布，利用贝叶斯公式转换成后验概率，根据最大后验概率得出推理结论。
    如公式1所示的贝叶斯公式中，事件Bi的概率为P（Bi），事件Bi已发生条件下事件A的概率为P（A|Bi），事件A发生条件下事件Bi的概率为P（Bi|A）。

    最大后验概率（Maximum a Posteriori assignment、MAP）是使后验概率达到最大值时的概率分布状态。它可以看做贝叶斯推理的一种特殊形式。在给定E=。的条件下，h为目标变量子集构成的一个联合状态赋值。如公式2所示。

    2 停车场车位引导模型
    将停车场按车辆行驶路径划分成不同区块，每个区块行驶路径两侧均包含不同数量的停车泊位。停车区块的集合为Pa，变量X ii E Pa，其中变量X。表示当前停车区块的状态。i标识路径是否畅通的状态，如i=0表示路不通，i=1表示路通。J标识当前变量区块空余车位状态，J=0表示无空余车位，j=1表示有空余车位。X11就表示此时段X区块状态为道路通畅且有空余车位。这样停车场内每个停车区块所处的状态都可用表1列出的状态所表示出来。

 
    设集合E为包含所有观察到有空余车位区块的集合，且E={ek|k=1，2，…，n}为空余车位区块数，则ek =X11 ，X11∈ Pa，ECPa。
    那么由停车场入口区块In到停车场区块ek的停车路径可表示为由UXij到e、的一个通路，其中UXij的约束条件是变量X为路径中排序在ek之前的区块。
    另一方面，对于优化停车进人泊位的整个过程并不是只由空车位和道路状况两个因素决定的，它还受到其它各种因素的相互影响，这些多种因素相互之间的影响关系可以通过贝叶斯网络表示出来。

    3 构建贝叶斯网络
    3.1变量选择
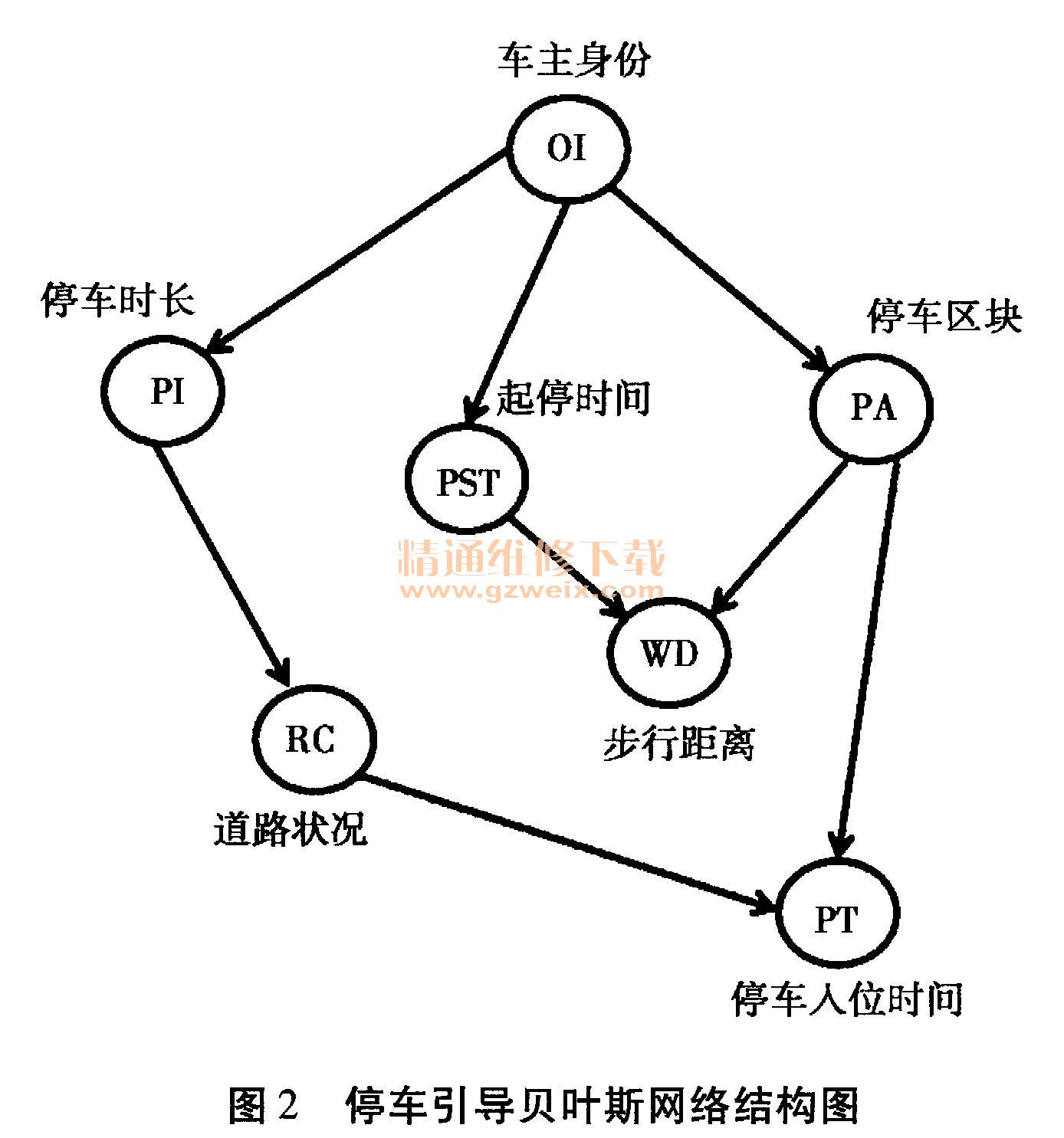
    考虑到停车行为受多种相关性因素的影响，同时结合北京市2016年停车场停车流量调查数据分析，选择了七个变量为贝叶斯网络构建的节点变量，分别是车主身份（ owner identity，01）、起停时间（parking start time，PST ）、停车时长（parking internval，PI）步行距离（walking distance、WD）、停车区域（parking area，PA）、停车人位时间（parkingtime ，PT）和道路状况（road condition，RC ） 。这些变量的取值情况如表2所示。

    3.2构建贝叶斯网络
    以北京市2016年停车场停车流量调查数据样木为训练数据集，通过应用贝叶斯网络经典的K2算法和Matlab的Full-BNT工具箱进行贝叶斯网络结构学习，确定如图2所示停车场车位引导贝叶斯网络的结构。

[1] [2]  下一页