摘要：针对复杂的电磁环境对跳频信号检测所产生的影响，提出了一种新的基于图像处理的跳频信号参数估计方法。首先将短时傅里叶变换（STFT）后的时频图处理为二维图像，然后根据电磁环境中噪声在时频图中的表现形式，对时频图进行滤波处理，最后根据对时频图的分析得出跳频信号参数估计。使用真实数据所进行的实验结果表明，所提出的方法能有效地滤除实际跳频信号中的雾态噪声、定频和突发信号，且不需要知道信号的跳速或驻留时间等前提条件，运算原理清晰，时间成本低且具有较高的准确度。目前该方法已应用于某数字接收机产品中，能很好地满足实际需求及测量精度要求。

    跳频通信具有良好的抗多径、抗衰落、抗干扰、低截获率和易于组网等特点，因此其在军事和民用通信方面得到了极大的应用和发展。

    由于多频率分量信号处理中被广泛使用的魏格纳威尔分布WVD（Wigner-Ville Distribution）会产生交叉项问题，严重影响信号检测结果，因此许多研究采用改进的WVD方法[1-3]，这些改进算法虽然能降低交叉项的影响，但运算量过大，且有的算法会导致时间分辨率及频率分辨率受到严重影响。参考文献[4]提出了一种基于自回归自适应谱估计模型的跳频信号检测方法；参考文献[5]提出利用信号STFT的结果得到其峰值序列来进行跳频信号的跳周期估计；参考文献[6]采用了时频分析与图像处理相结合的算法，有效地通过图像分割等技术提取出了跳频信号，但由于未考虑到实际环境中所存在的噪声干扰等问题对跳频信号检测的影响，使其实用性受到局限。

    本文提出用短时傅里叶变换（STFT）对跳频信号进行分析，利用现在较为完善的图像处理技术与时频分析相结合，滤除杂散噪声及定频、突发号，再根据时频图中信号在时间轴和频率轴上的投影求出频率集，利用跳时刻差分的均值来估计跳周期并通过实验给出了估计性能。并且目前大多数文章所提出的方法都只是建立在仿真分析的基础上，缺乏实际应用验证。而本文提出的方法已应用于实际产品中，其稳定性和精度均能满足需求，具有较高的实际意义。

1跳频信号的检测及分析

1.1短时傅里叶变换

    跳频信号是一种非平稳信号，传统的傅里叶变换对它的处理具有信号的时域与频域信息不能同时局部化等局限性。而时频分析[7]作为分析时变非平稳信号的有力工具，近年来受到越来越多的重视，已成为跳频通信研究中常用的分析手段。其中STFT计算量小、时频聚集性较好，从时频图中可以较为明确地分析信号特征，应用最为广泛。

    在实际中，信号往往是离散的，所以通常使用离散的短时傅里叶变换来对信号进行处理。离散短时傅里叶变换（DSTFT）定义如下：

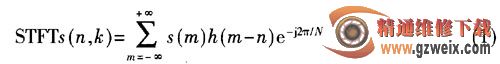
式中，s (m)是离散时间信号，h (n)是窗函数，N是离散傅里叶变换的总点数。从式(1)可以看出，设每个窗口的长度为ns，则STFT变换相当于把信号分为nt=N/ns个时间窗，对每个窗内的信号进行FFT变换。对时频谱图定义为STFT模的平方，其表达式为：

    根据W. Heisenberg不确定性原理，短时傅里叶变换的时间分辨率和频率分辨率互相矛盾，应当根据实际情况来考虑时间分辨率及频率分辨率的大小。对非平稳信号，若信号变化剧烈，要求窗函数有较高的时间分辨率；而波形变化比较平缓时，则要求窗函数有较高的频率分辨率。因此，窗函数的选取十分重要，窗越宽，时间分辨率越差；反之则会降低频率分辨率。

1.2对时频图进行图像处理

    通过短时傅里叶变换得到的时频图，可以将其视为一幅二维图像。复杂的电磁环境中存在许多噪声会对跳频信号的检测造成较大干扰，而这些噪声信号在时频图中的表现形式各有不同。在时频图中不同频率上彼此衔接的短线段为跳频信号，每一段短线段即为一跳；图中除跳频信号外，在同一频率连续出现的长线段为定频信号；一系列较细的斜线段为扫频信号；由噪声的随机性产生的雾态噪声，在时频图上为随机分布的零散能量。因此，从实际环境中剔除噪声信号演变成为对时频图进行图像相关处理。

    数学形态学是基于集合论的图像处理分析方法，可以保持所需图形的基本形状特性，并除去不相干的结构，并且可以大大提高图像分析和处理的速度。本文选用其中的开、闭运算来对时频图进行滤波处理。

    在形态学图像处理中，被处理的图像为目标图像X，用来进行处理操作的图像称为结构元素B。则腐蚀可定义为：

    在形态学中，先腐蚀后膨胀称为开运算。开运算可以用来对较大的物体边界进行平滑且不明显改变其面积，并消除较小的图像结构。假设经过二值化后的时频图为X，结构元素为B，取B的宽度和高度分别小于跳频信号每跳的驻留时间和瞬时带宽，便可利用开运算的这种特性，滤除在时频图中表现为随机零散能量的雾态噪声。下式中的X。即为滤去雾态噪声后的时频图：

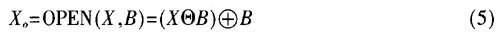
    先膨胀后腐蚀的运算称为闭运算。闭运算可以连接邻近的物体，并且填充物体内的空洞。对时频图进行闭运算，用于提取出其中的定频信号及突发信号。式(6)中的Xc为被提取出来的定频信号和突发信号。

    在滤除雾态噪声后的时频图Xo中去除定频信号及突发信号，便可最终得到跳频信号Xh，其中＆是做与运算，Xc是Xc求反：

[1] [2] [3]  下一页