无论在何处，只要存在两个电流回路，就会有互感。一个回路的电流产生一个磁场，而该磁场会影响第二个回路。两个回路相互作用，其相互作用的系数随距离的增加快速地减小。两个回路之间相互作用的系数称为它们的互感，单位是亨利（H），或伏-秒/安培。两个电路之间的互感耦合相当于一个连接在电路A和电路B之间的微小变压器，如图1.18所示。无论何处，对于两个相邻电流回路的相互作用，可以看成是一个变压器的初级和次级，从面得到互感。

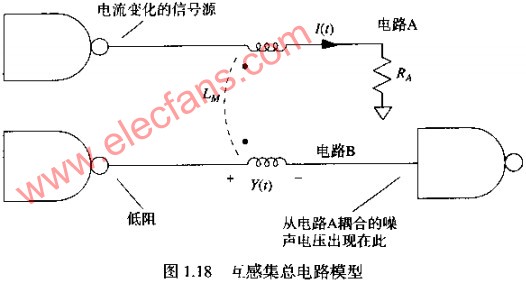
互感LM将一个噪声电压Y注入到电路B，按照下列规则，噪声电压Y与电路A中的电流变化速率成正比：Y=LM DIA/DT

回路A中电流的快速变化导致回路B上产生一个相当大的电压，高速设计中互感耦合的重要性由此面来。

对于实际的耦合噪声电压，式（Y=LM DIA/DT）只是一个简单的近似公式。完整的公式应该采用初级和次级电路之间的电流差，以及初级和次级线圈对电路的负载效应。关于式（Y=LM DIA/DT）的前提假设，与式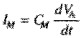的情况类似，即：

1、LM上的感应电压远远小于原有信号的电压。由此附加的LM不增加电路A的负载。在数字产品中，由感耦合产生的噪声电压总是比源信号小。

2、电路B中的耦合信号电流小于电路A中的电流。可以忽略电路B中小的耦合电流，并假设耦合变压器的初级和次级的电流差正好等于IA。

3、假设与电路B的接地阻抗相比，次级的阻抗很小，只在电路B的电压上加上耦合噪声电压，这个过程忽略了互感和次级电路之间的相互作用。

与互容类似，数字电路中的互感，通常导致电路之间不必要的串扰。

图1.19举例说明了互感耦合起作用的过程：

1、回路A中的任何电流都会产生一个磁场能量图。回路中的电流越强，存储在回路A周围单位空间中的电磁能越大。

2、我们可以通过回路B所包围的总面积计算来自回路A的总磁场强度。回路B的面积上的总磁场强度，称为B的磁场通量，它最回路A和回路B的距离、其实际比例以及相对方向的一个函数，并且直接与A中的电流成正比，A中的电流越大，B的磁通量也越大。

3、回路A中电流的变化会相应成比例地改变通过回路B的磁通量。

4、法拉第定律告诉我们，回路B中的感应电压与通过回路B的磁通量变化率成正比。

把1至4的概念结合起来，会发现回路B中的感应电压与回路A中的电流变化率成正比，该比例常数称为电路A和B之间的互感。

因为磁场是个矢量，回路B翻转将导致耦合磁通的极性发生反向。耦合的噪声电压极性也发生反向。回路A的翻转将导致同样的结果。如果使回路B与磁场的磁力线方向平行，将导致通过回路B的总磁通量为零，且耦合噪声也为零。与互容耦合不同，互感耦合有可能产生一个与驱动信号极性相反的串扰，它对环路的方向同样非常敏感。