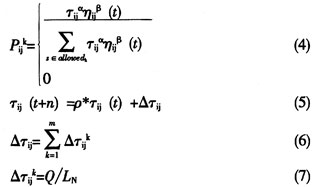蚁群算法的基本公式如下：



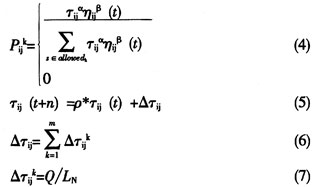
2.2 混沌蚁群算法

混沌蚁群算法(CACO)是受到自然界蚂蚁走行的混沌特点和整个种群的自组织特点的启发。它利用混沌的遍历性和随机性等特点来将混沌扰动算子引入蚁群算法，并将带有混沌特征的初始化变量线性映射到变量取值区间。该方法兼顾了混沌动态搜索和智能搜索的特点，可有效地避免搜索过程中陷入局部最优，从而达到提高算法速度和全局寻优的能力。

(1)混沌初始化

设τ_ij(t)为t时刻路径上的信息浓度，利用混沌运动的遍历性进行混沌初始化。混沌变量选择典型的混沌系统Logistic映射迭代公式如下：



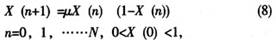
式中，μ为控制参数，当μ=4时，Logistic完全处于混沌状态，此时系统在[0，1]之间具有遍历性。如果利用全排列理论将每个混沌变量对应于一条路径，也就是为每条路段上的信息素浓度根据混沌量给定初始值τ_ij(0)，就可以有效地解决基本蚁群算法收敛速度慢的问题。

(2)引入混沌扰动量

在蚁群算法中，如果蚂蚁后从点i至某一点j，则在路径ij上留下信息素τ_ij(t)。蚂蚁k在走完任意一路径以后，将按式(5)更新该路径上的信息素。可以看出，此更新方法在加快寻优的同时，却容易陷入局部最优解。因此，在此处引入混沌扰动量来调整信息素，以使其避免陷入局部最优极值区间。改进后的式子为：



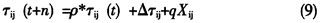
其中，X_ij为混沌扰动量，可采用典型混沌系统Logistic映射得到，q为相关系数。

2.3  混沌蚁群算法的实现步骤

实现混沌蚁群算法的具体步骤如下：

Step1：初始化BP网络结构，设定网络的输入层、隐含层、输出层的神经元个数；

Step2：混沌初始化信息素浓度、个体最优和全局最优；

Step3：用公式(4)计算每只蚂蚁的转移概率；

Step4：根据每只蚂蚁的转移概率得出本次最优路径并最优值比较，若更优，则更新最优值；

Step5：将每只蚂蚁的最优值与整个蚁群的最优值相比较，若更优，则其将成为整个蚁群新的最优值；

Step6：更新并按公式(9)修改路径ij上的信息素浓度；

Step7：比较次数是否达到预设的精度，若满足预设精度，则最后一次迭代的全局最优值中每一维的权值和阈值就是所求的；否则返回step3，算法继续迭代，直至满足条件为止。

3 基于DTC的系统仿真

3.1 直接转矩控制系统结构

直接转矩控制(DTC)系统的结构原理如图2所示。在α-β坐标系下，通过获得定子电压U_sα、U_sβ，定子电流I_sα、I_sβ及定子电流导数pI_sα、pI_sβ归一化后，即可构成神经网络的六个输入，再经过反归一化，即可得到转子转速ω，从而构建一个动态转速估计器。

上一页  [1] [2] [3]