为什么使用DSP?DSP架构以及DSP与传统模拟电路相比所具有的优势
Why Use DSP?
Having heard a lot about digital signal processing (DSP) technology, you may have wanted to find out what CAN be done with DSP, investigate why DSP is preferred to analog circuitry for many types of operations, and discover how to learn enough to design your own DSP system. This artICle, the first of a series, is an opportunity to take a substantial first step towards finding answers to your questions. This series is an introduction to DSP topics from the point of view of analog system designers seeking additional tools for handling analog signals. Designers reading this series can learn about the possibilities of DSP to deal with analog signals and where to find additional sources of information and assistance.
What is [a] DSP? In brief, DSPs are processors or microcomputers whose hardware, SOFtware, and instruction sets are optimized for high-speed numeric processing applications an essential for processing digital data representing analog signals in real time. What a DSP does is straightforward. When acting as a digital fiLTEr, for example, the DSP receives digital values based on samples of a signal, calculates the results of a filter function operating on these values, and provides digital values that represent the filter output; it can also provide system control signals based on properties of these values. The DSP’s high-speed arithmetic and logical hardware is programmed to rapidly execute algorithms modelling the filter transformation.
The combination of design elements arithmetic operators, memory handling, instruction set, parallelism, data addressing that provide this ability forms the key difference between DSPs and other kinds of processors. Understanding the relationship between real-time signals and DSP calculation speed provides some background on just how special this combination is. The real-time signal comes to the DSP as a train of individual samples from an analog-to-digital converter (ADC). To do filtering in real-time, the DSP must complete all the calculations and operations required for processing each sample (usually updating a process involving many previous samples) before the next sample arrives. To perform high-order filtering of real-world signals having significant Frequency content calls for really fast processors. WHY USE A DSP?
To get an idea of the type of calculations a DSP does and get an idea of how an analog circuit compares with a DSP system, one could compare the two systEMS in terms of a filter function. The familiar analog filter uses resistors, caPACitors, inductors, amplifiers. It can be cheap and easy to assemble, but difficult to calibrate, modify, and maintain a difficulty that increases exponentially with filter order. For many purposes, one can more eaSILy design, modify, and depend on filters using a DSP because the filter function on the DSP is software-based, flexible, and repeatable. Further, to create flexibly adjustable filters with higher-order response requires only software modifications, with no additional hardware unlike purely analog circuits. An ideal bandpass filter, with the frequency response shown in Figure 1, would have the following characteristics:
As Figure 1 shows, an analog approach using second-order filters would require quite a few staggered high-Q sections; the difficulty of tuning and adjusting it can be imagined.
`

Figure 1. An ideal bandpass filter and second-order approximations.
With DSP software, there are two basic approaches to filter design: finiteimpulse response (FIR) and infinite impulse response (IIR). The FIR filter’s time response to an impulse is the straightforward weighted sum of the present and a finite number of previous input samples. Having no feedback, its response to a given sample ends when the sample reaches the “end of the line” (Figure 2). An FIR filter’s frequency response has no poles, only zeros. The IIR filter, by comparison, is calLED infinite because it is a recursive function: its output is a weighted sum of inputs and outputs. Since it is recursive, its response can continue indefinitely. An IIR filter frequency response has both poles and zeros.

Figure 2. Filter equations and delay-line representation.
The xs are the input samples, ys are the output samples, as are input sample weightings, and bs are output sample weightings. n is the present sample time, and M and N are the number of samples programmed (the filter’s order). Note that the arithmetic operations inDICated for both types are simply sums and products in potentially great number. In fact, multiply-and-add is the case for many DSP algorithms that represent mathematical operations of great sophistication and complexity.
Approximating an ideal filter consists of applying a transfer function with appropriate coefficients and a high enough order, or number of taps (considering the train of input samples as a tapped delay line). Figure 3 shows the response of a 90-tap FIR filter compared with sharp-cutoff Chebyshev filters of various orders. The 90-tap example suggests how close the filter can come to approximating an ideal filter. Within a DSP system, programming a 90-tap FIR filter like the one in Figure 3 is not a difficult task. By comparison, it would not be cost-effective to attempt this level of approximation with a purely analog circuit. Another crucial point in favor of using a DSP to approximate the ideal filter is long-term stability. With an FIR (or an IIR having sufficient resolution to avoid truncation-error buildup), the programmable DSP achieves the same response, time after time. Purely analog filter responses of high order are less stable with time.

Figure 3. 90-tap FIR filter response compared with those of sharp cutoff Chebyshev filters.
Mathematical transform theory and practice are the core requirement for creating DSP applications and understanding their limits. This article series walks through a few signal-analysis and -processing examples to introduce DSP concepts. The series also provides references to texts for further study and identifies software tools that ease the development of signal-processing software. SAMPLING REAL-WORLD SIGNALS
Real-world phenomena are analog the continuously changing energy levels of physical processes like sound, light, heat, eleCTRicity, magnetism. A transducer converts these levels into manageable electrical voltage and current signals, and an ADC samples and converts these signals to digital for processing. The conversion rate, or sampling frequency, of the ADC is critically important in digital processing of real-world signals.
This sampling rate is determined by the amount of signal information that is needed for processing the signals adequately for a given application. In order for an ADC to provide enough samples to aCCurately describe the real-world signal, the sampling rate must be at least twice the highest-frequency component of the analog signal. For example, to accurately describe an audio signal containing frequencies up to 20 kHz, the ADC must sample the signal at a minimum of 40 kHz. Since arriving signals can easily contain component frequencies above 20 kHz (including noise), they must be removed before sampling by feeding the signal through a low-pass filter ahead of the ADC. This filter, known as an anti-aliasing filter, is intended to remove the frequencies above 20 kHz that could corrupt the converted signal.
However, the anti-aliasing filter has a finite frequency rolloff, so additional bandwidth must be provided for the filter’s transition band. For example, with an input signal bandwidth of 20 kHz, one might allow 2 to 4 kHz of extra bandwidth.

Figure 4. Antialiasing filter ideal response.
Figure 4 depicts the filter needed to reject any signals with frequencies above half of a 48-kHz sampling rate. Rejection means attenuation to less than 1/2 least-significant bit (LSB) of the ADC’s resolution. One way to achieve this level of rejection without a highly sophisticated analog filter is to use an oversamplingconverter, such as a sigma-delta ADC. It typically obtains low-resolution (e.g., 1-bit) samples at megahertz rates much faster than twice the highest frequency component greatly easing the requirement for the analog filter ahead of the converter. An internal digital filter (DSP at work!) restores the required resolution and frequency response. For many applications, oversampling converters reduce system design effort and cost. PROCESSING REAL-WORLD SIGNALS
The ADC sampling rate depends on the bandwidth of the analog signal being sampled. This sampling rate sets the pace at which samples are available for processing. Once the system bandwidth requirements have established the A/D converter sampling rate, the designer can begin to explore the speed requirements of the DSP processor.
Processing speed at a required sample rate is influenced by algorithm complexity. As a rule, the DSP needs to finish all operations relating to the first sample before receiving the second sample. The time between samples is the time budget for the DSP to perform all processing tasks. For the audio example, a 48-kHz sampling rate corresponds to a 20.833-µs sampling interval. Figure 5 relates the analog signal and digital sampling rate.

Figure 5. Sampling train and processing time.
Next consider the relation between the speed of the DSP and complexity of the algorithm (the software containing the transform or other set of numeric operations). Complex algorithms require more processing tasks. Because the time between samples is fixed, the higher complexity calls for faster processing. For example, suppose that the algorithm requires 50 processing operations to be performed between samples. Using the previous example’s 48-kHz sampling rate (20.833-µs sampling interval), one can calculate the minimum required DSP processor speed, in millions of operations per second (MOPS) as follows:
Thus if all of the time between samples is available for operations to implement the algorithm, a processor with a performance level of 2.4 MOPS is required. Note that the two common ratings for DSPs, based on operations per second (MOPS) and instructions per second (MIPS), are not the same. A processor with a 10-MIPS rating that can perform 8 operations per instruction has basically the same performance as a faster processor with a 40 MIPS rating that can only perform 2 operations per instruction. SAMPLING VARIOUS REAL-WORLD SIGNALS
There are two basic ways to acquire data, either one sample at a time or one frame at a time (continuous processing vs. batch processing). Sample-based systems, like a digital filter, acquire data one sample at a time. As shown in Figure 6, at each tick of the cLOCk, a sample comes into the system and a processed sample is output. The output waveform develops continuously.

Figure 6. Example of continuous processing of samples in digital filter.
Frame-based systems, like a spectrum analyzer, which determines the frequency components of a time-varying waveform, acquire a frame (or block of samples). Processing occurs on the entire frame of data and results in a frame of transformed data, as shown in Figure 7.

Figure 7. Example of batch processing of a block of data.
For an audio sampling rate of 48 kHz, a processor working on a frame of 1024 samples has a frame acquisition interval of 21.33 ms (i.e., 1024 x 20.833 µs = 21.33 ms). Here the DSP has 21.33 ms to complete all the required processing tasks for that frame of data. If the system handles signals in real time, it must not lose any data; so while the DSP is processing the first frame, it must also be acquiring the second frame. Acquiring the data is one area where special architectural features of DSPs come into play: Seamless data acquisition is facilitated by a processor’s flexible data-addressing capabilities in conjunction with its direct memory-accessing (DMA) channels. RESPONDING TO REAL-WORLD SIGNALS
One cannot assume that all the time between samples is available for the execution of processing instructions. In reality, time must be budgeted for the processor to respond to external devices, controlling the flow of data in and out. Typically, an external device (such as an ADC) signals the processor using an interrupt. The DSP’s response time to that interrupt, or interrupt latency, directly influences how much time remains for actual signal processing.
Interrupt latency (response delay) depends on several factors; the most dominant is the DSP architecture’s instruction pipelining. An instruction pipeline consists of the number of instruction cycles that occur between the time an interrupt is received and the time that program execution resumes. More pipeline levels in a DSP result in longer interrupt latency. For example, if a processor has a 20-ns cycle time and requires 10 cycles to respond to an interrupt, 200 ns elapse before it executes any signal-processing instructions.
When data is acquired one sample at a time, this 200-ns overhead will not hurt if the DSP finishes the processing of each sample before the next arrives. When data is acquired sample-by-sample while processing a frame at a time, however, an interrupted system wastes processor instruction cycles. For example, a system with a 200-ns interrupt response time running a frame-based algorithm, such as the FFT, with a frame size of 1024 samples, would require 204.8 µs of overhead. That amounts to more than 10,000 instruction cycles wasted to latency productive time when the DSP could be performing signal processing. This waste is easy to avoid in DSPs having architectural features such as DMA and dual memory access; they let the DSP receive and store data without interrupting the processor. DEVELOPING A DSP SYSTEM
Having discussed the role of the processor, the ADC, the anti-aliasing filter, and the timing relationships between these components, it is time to look at a complete DSP system. Figure 8 shows the building blocks of a typical DSP system that could be used for data acquisition and control.

Figure 8. Putting together elements of a DSP system.
Note how few components make up the DSP system, because so much of the system’s functionality comes from the programmable DSP. Converters funnel data into and out of the DSP; the ADC timing is controlled by a precise sampling clock. To simplify system design, many converter devices available today combine some or all of the following: an A/D converter, a D/A converter, a sampling clock, and filters for anti-aliasing and anti-imaging. The clock oscillator in these types of I/O components is separately controlled by an external Crystal. Here are some important points about the data flow in this sort of DSP system:
Analog Input: The analog signal is appropriately band-limited by the anti-aliasing filter and applied to the input of the ADC. At the selected sampling time, the converter interrupts the DSP processor and makes the digital sample available. The choice between serial and parallel interfacing between the ADC and DSP depends on the amount of data, design complexity trade-offs, space, power, and price.
Digital Signal Processing: The incoming data is handled by the DSP’s algorithm software. When the processor completes the required calculations, it sends the result to the DAC. Because the signal processing is programmable, considerable flexibility is available in handling the data and improving system performance with incremental programming adjustments.
Analog Output: The DAC converts the DSP’s output into the desired analog output at the next sample clock. The converter’s output is smoothed by a low-pass, anti-imaging filter (also called a reconstruction filter), to produce the reconstructed analog signal.
Host Interface: An optional host interface lets the DSP communicate with external systems, sending and receiving data and control information. REVIEW AND PREVIEW
The goal of this article has been to provide an overview of major DSP design concepts and explain some of the reasons why a DSP is better suited that analog circuitry for some applications. The issues introduced in this article include:
Because these issues involve many valuable levels of detail that we could not do justice to in this brief article, you should consider reading Richard Higgins’s text, Digital Signal Processing in VLSI (see References below). This text provides a complete overview of DSP theory, implementation issues, and reduction to practice (with devices available at the time it was published), plus exercises and examples. The Reference section below also contains other sources that further amplify this article’s issues. To prepare for the next articles in this series, you might want to get free copies of the ADSP-2100 Family User’s Manual* and the ADSP-2106x SHARC User’s Manual.* These texts provide information on Analog Devices’s fixed- and floating-point DSP architectures, a major topic in these articles. The next article will cover the following territory:
If you've read Part 1 of this series (or are already familiar with some of the ways a DSP can work with real-world signals), you might want to learn more about how digital filters (such as those described in Part 1) can be implemented with a DSP.This article, the second of a series, introduces the following DSP topics:
This series seeks to describe these topics from the perspective of analog system designers who want to add DSP to their design repertoire. Using the information from articles in this series as an introduction, designers can make more informed decisions about when DSP designs might be more productive than analog circuits.
Modeling Filter Transform Functions
Part 1 compared analog and digital filter properties and suggested why one might implement these filters digitally (using DSP); this part focuses on some of the mechanics of digital filter application.
The three principal reasons for using digital filtering are (1) closer approach to ideal filter approximations, (2) ability to adjust filter characteristics in software rather than by physical tuning, and (3) compatibility of filter response with sampled data. The two best-known filters described in Part 1 are the finite impulse-response (FIR) and infinite impulse-response (IIR) types. The FIR filter response is called finite because its output is based solely on a finite set of input samples; it is non-recursive and has no poles, only zeroes in its s-plane.The IIR filter, on the other hand, has a response that can go on indefinitely (and can be unstable) because it is recursive, i.e., its output values are affected by both input and output. It has both poles and zeroes in its s-plane. Figure 1 shows the typical filter architectures and summation formulas that appeared in Part 1.

Figure 1.Filter equations and their delay-line models.
To model these filters digitally, one might take two steps. First, view these formulas as programs running on a computer. This step consists of breaking down the formula into the mathematical steps (e.g., multiply and add) and identifying all of the additional operations that would be necessary for a computer to perform (handling instructions and data, testing status, etc.) to implement the formula in software.
Second, take those operations and write them as a program.This can be a fairly arduous task. Fortunately, there is much "canned" software available, often in a high-level language (HLL) such as C, somewhat simplifying (but by no means eliminating!) the job of programming. From the point of view of learning, though, it may be more instructive to start with assembly language; also assembly language algorithms are often more useful than HLL where system performance must be optimized. At the level of abstraction of some high-level languages, the program may not look much like the equations. For example, Figure 2 shows an example of an FIR algorithm implemented as a C program.*
float fir_filter(float input, float *coef, int n, float *history)
{
int i;
float *hist_ptr, *hist1_ptr, *coef_ptr;
float output;
hist_ptr = history;
hist1_ptr = hist_ptr; /* use for history update */
coef_ptr = coef + n -1; /* point to last coef */
/*form output accumulation */
output = *hist_ptr++ * (*coef_ptr-);
for(i = 2; i < n; i++)
{
*hist1_ptr++ = *hist_ptr; /* update history array */
output += (*hist_ptr++) * (*coef_ptr-);
}
output += input * (*coef_ptr); /* input tap */
*hist1_ptr = input; /* last history */
return(output);
}
Figure 2.FIR Filter as C program.
There are many analysis packages available that support algorithm modeling; see the references at the end of this article for several popular packages.We will return to algorithm modeling at various times in the course of this series. Now, continuing the discussion of the process, after these filter algorithms have been modeled, they are ready for implementation in DSP architecture.
Relating The Models To DSP Architecture: For programming, one must understand four sections of DSP architecture: numeric, memory, sequencer, and I/O operations. This architectural discussion is generic (applying to general DSP concepts), but it is also specific as it relates to programming examples later in this article. Figure 3 shows the generalized DSP architecture that this section describes.
ARCHITECTURE
Numeric Section: Because DSPs must complete multiply/accumulate, add, subtract, and/or bit-shift operations in a single instruction cycle, hardware optimized for numeric operations is central to all DSP processors. It is this hardware that distinguishes DSPs from general-purpose microprocessors, which can require many cycles to complete these types of operations. In the digital filters (and other DSP algorithms), the DSP must complete multiple steps of arithmetic operations involving data values and coefficients, to produce responses in real time that have not been possible with general-purpose processors.
Numeric operations occur within a DSP's multiply/accumulator (MAC), arithmetic-logic unit (ALU), and barrel shifter (shifter). The MAC performs sum-of-products operations, which appear in most DSP algorithms (such as FIR and IIR filters and fast Fourier transforms). ALU capabilities include addition, subtraction, and logical operations. Operations on bits and words occur within the shifter. Figure 3 shows the parallelism of the MAC, ALU, and shifter and how data can flow into and out of them.

Figure 3.A useful DSP architecture.
From a programming point of view, a DSP architecture that uses separate numeric sections provides great flexibility and efficiency. There are many non-conflicting paths for data, allowing single-cycle completion of numeric operations. The architecture of the DSP must also provide a wide dynamic range for MAC operations, with the ability to handle multiplication results that are double the width of the inputs-and accumulator outputs that can mount up without overflowing. (On a 16-bit DSP, this feature equates to 16-bit data inputs and a 40-bit result output from the MAC.) One needs this range for handling most DSP algorithms (such as filters).
Other features of the numeric section can facilitate programming in real-time systems. By making operations contingent on a variety of conditional states, which result from numeric operations, these can serve as variables in a program's execution, testing for carries, overflows, saturates, flags, or other states. Using these conditionals, a DSP can rapidly handle decisions about program flow based on numeric operations. The need to be constantly feeding data into the numeric section is a key design influence on the DSP's memory and internal bus structures.
Memory Section: DSP memory and bus architecture design is guided by the need for speed. Data and instructions must flow into the numeric and sequencing sections of the DSP on every instruction cycle. There can be no delays, no bottlenecks. Everything about the design focuses on throughput.
Etymology of Harvard and von Neumann Architectures- According to John A. N. Lee, Department of Computer Science, Virginia Tech: "Howard Aiken, developer of the Harvard series of machines, insisted on the separation of data and programs in all his machines. In the Mark III, which I know best, he even had different size drums for each." "The von Neumann concept was that by treating instructions as data one could make alterations in programs, enhancing the ability for programs to 'learn'." "For some reason, the latter was given von Neumann's name, while the former took its name from the Harvard line of machines." |
To put this focus on throughput in perspective, one can look at the difference between DSP memory design and memory for other microprocessors. Most microprocessors use a single memory space containing both data and instructions, using one bus for address and other for data or instructions. This architecture is called von Neumann architecture. The limitation on throughput in a von Neumann architecture comes from having to choose between either a piece of data or an instruction on each cycle. In DSPs, memory is typically divided into program and data memory-with separate busses for each. This type of architecture is referred to as Harvard architecture. By separating the data and instructions, the DSP can fetch multiple items on each cycle, doubling throughput. Additional optimizations, such as instruction cache, results feedback, and context switching also increase DSP throughput.
Other optimizations in DSP memory architecture relate to repeated memory accesses. Most DSP algorithms, such as digital filters, need to get data from memory in a repeating pattern of accesses. Typically, this type of access serves to fetch data from a range of addresses, a range that is filled with data from the real-world signals to be processed. By reducing the number of instructions needed to "manage" memory accesses (overhead), DSPs "save" instruction cycles, allowing more time for the main job of each cycle-processing signals. To reduce overhead and automatically manage these types of accesses, DSPs utilize specialized data address-generators (DAGs).
Most DSP algorithms require two operands to be fetched from memory in a single cycle to become inputs to the arithmetic units. To supply the addresses of these two operands in a flexible manner, the DSP has two DAGs. In the DSP's modified Harvard architecture, one address generator supplies an address over the data-memory address bus; the other supplies an address over the program-memory address bus. By performing these two data fetches in time for the next numeric instruction, the DSP is able to sustain single-cycle execution of instructions.
DSP algorithms, such as the example digital filters, usually require data in a range of addresses (a buffer) to be addressed so that the address pointer "wraps-around" from the end of the buffer back to the start of the buffer (buffer length). This pointer movement is called circular buffering. (In the filter equations, each summation basically results from a sequence of multiply-and-accumulates of a circular buffer of data points and a circular buffer of coefficients). A variation of circular buffering, which is required in some applications, advances the address pointer by values greater than one address per "step," but still wraps around at a given length. This variation is called modulo circular buffering.
By supporting various types of buffering with its DAGs, the DSP is able to perform address modify and compare operations in hardware for optimum efficiency. Performing these functions in software (as occurs in general purpose processors) limits the processor's ability to handle real-time signals.
Because buffering is an unusual concept, yet key to digital signal processing, a brief buffering example is useful. In the example illustrated in Figure 4, a buffer of eight locations resides in memory starting at address 30. The address generator must calculate next addresses that stay within this buffer yet keep the proper data spacing so that two locations are skipped. The address generator outputs the address 30 on to the address bus while it modifies the address to 33 for the next cycle's memory access. This process repeats, moving the address pointer through the buffer. A special case occurs when the address 36 gets modified to 39. The address 39 is outside the buffer. The address generator detects that the address has fallen outside of the buffer boundary and modifies the address to 31 as if the end of the buffer is connected to the start of the buffer. The update, compare, and modify occur with no overhead. In one cycle, the address 36 is output onto the address bus. On the next cycle, the address 31 is output onto the address bus. This modulo circular buffering serves the needs of algorithms such as interpolation filters and saves instruction cycles for processing.
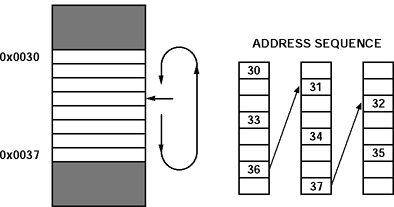
Figure 4.Example of modulo circular buffering.
Sequencer Section: Because most DSP algorithms (such as the example filters) are by nature repetitive, the DSP's program sequencer needs to loop through the repeated code without incurring overhead while getting from the end of the loop back to the start of the loop. This capability is called zero-overhead looping. Having the ability to loop without overhead is a key area in which DSPs differ from conventional microprocessors. Typically, microprocessors require that program loops be maintained in software, placing a conditional instruction at the end of the loop. This conditional instruction determines whether the address pointer moves (jumps) back to the top of the loop or to another address. Because getting these addresses from memory takes time- and availability of time for signal-processing is critical in DSP applications-DSPs cannot waste cycles retrieving addresses for conditional program sequencing (branching) in this manner. Instead, DSPs perform these test and branch functions in hardware, storing the needed addresses.
As Figure 5 shows, the DSP executes the last instruction of the loop in one cycle. On the next cycle, the DSP evaluates the conditional and executes either the first instruction at the top of the loop or the first instruction outside the loop. Because the DSP uses dedicated hardware for these operations, no extra time is wasted with software evaluating conditionals, retrieving addresses, or branching program execution. 
Figure 5.Example of program loop.
Input/Output (I/O) Section: As noted again and again, there is a need for tremendous throughput of data to the DSP; everything about its design is focused on funneling data into and out of the numeric, memory, and sequencer sections. The source of the data- and destination of the output (the result of signal processing)-is the DSP's connection to its system and the real-world. A number of I/O functions are required to complete signal processing tasks. Off-DSP memory arrays store processor instructions and data. Communication channels (such as serial ports, I/O ports and direct memory accessing (DMA) channels transfer data into and out of the DSP quickly. Other functions (such as timers and program boot logic) ease DSP system development. A brief list of typical I/O tasks in a DSP system includes the following (among many others):
EXPERIMENTING WITH DIGITAL FILTERS
Having modeled the filter algorithms and looked at some of the DSP architectural features, one is ready to start looking at how these filters could be coded in DSP assembly language. Up to this point the discussion and examples have been generic, applying to almost all DSPs. Here, the example is specific to the Analog Devices ADSP-2181. This processor is a fixed-point, 16-bit DSP. The term "fixed-point" means that the "point" separating the mantissa and exponent does not change its bit location during arithmetic operations. Fixed-point DSPs can be more challenging to program, but they tend to be less expensive than floating-point DSPs. The "16-bit" in "16-bit DSP" refers to the size of the DSP's data words. This DSP uses 16-bit data words and 24-bit wide instruction words. DSPs are specified by the size of the data, rather than instruction width because data word size describes the width of data that the DSP can handle most efficiently.
The example program in Figure 6 is an FIR filter in ADSP-2181 assembly language. The software has two parts. The main routine includes register and buffer initialization along with the interrupt vector table, and the interrupt routine that executes when a data sample is ready. After initialization, the DSP executes instructions in the main routine, performing some background tasks, looping through code, or idling in a low-power standby mode until it gets an interrupt from the A/D converter. In this example, the processor idles in a low-power standby mode waiting for an interrupt.
The FIR filter interrupt subroutine (the last segment of code) is the heart of the filter program. The processor responds to the interrupt, saving the context of the main routine and jumping to the interrupt routine. This interrupt routine processes the filter input sample, reading data and filter coefficients from memory and storing them in data registers of the DSP processor. After processing the input sample, the DSP sends an output sample to the D/A converter.
.module/RAM/ABS=0 FIR_PROGRAM; Note that this program uses DSP features that perform operations with zero overhead, usually introduced by a conditional. In particular, program loops and data buffers are maintained with zero overhead. The multifunction instruction in the core of the filter loop performs a multiply/accumulate operation while the next data word and filter coefficient are fetched from memory. The program checks the final result of the filter calculation for any overflow. If the final value has overflowed, the value is saturated to emulate the clipping of an analog signal. Finally, the context of the main routine is restored and the instruction flow is returned to the main routine with a return from interrupt (RTI) instruction. REVIEW AND PREVIEW Because these issues involve many valuable levels of detail that one could not do justice to in this brief article, you should consider reading Richard Higgins's text, Digital Signal Processing in VLSI, and Paul Embree's text, C Algorithms For Real Time DSP (see References below). These texts provides a complete overview of DSP theory, implementation issues, and reduction to practice (with devices available at the time of publication), plus exercises and examples. The Reference section below also contains other sources that further amplify this article's issues. To prepare for the next articles in this series, you might want to get free copies of the ADSP-2100 Family User's Manual* or the ADSP-2106x SHARC User's Manual.* These texts provide information on Analog Devices's fixed- and floating-point DSP architectures, a major topic in these articles. Working through this series, each part adds some feature or information contributing to the series goal of developing a DSP system. To reach this goal, the next article describes the series' development platform (the ADSP-2181 EZ-KIT LITE) and introduces additional DSP development topics. So far, we have described the physical architecture of the DSP processor, explained how DSP can provide some advantages over traditionally analog circuitry, and examined digital filtering, showing how the programmable nature of DSP lends itself to such algorithms. Now we look at the process of implementing a finite-impulse- response (FIR) filter algorithm (briefly introduced in Part 2, implemented in ADSP-2100 Family assembly code) on a hardware platform, the ADSP-2181 EZ-Kit Lite&tm;. The implementation is expanded to handle data I/O issues. USING DIGITAL FILTERS Many of the architectural features of the DSP, such as the ability to perform zero-overhead loops, and to fetch two data values in a single processor cycle, will be useful in implementing this filter. Reviewing briefly, an FIR filter is an all-zeros filter that is calculated by convolving an input data-point series with filter coefficients. Its governing equation and direct-form representation are shown in Figure 1. In this structure, each "z? " box represents a single increment of history of the input data in z-transform notation. Each of the successively delayed samples is multiplied by the appropriate coefficient value, h(m), and the results, added together, generate a single value representing the output corresponding to the nth input sample. The number of delay elements, or filter taps, and their coefficient values, determine the filter抯 performance. The filter structure suggests the physical elements needed to implement this algorithm by computation using a DSP. For the computation itself, each output sample requires a number of multiply-accumulate operations equal to the length of the filter. The delay line for input data and the coefficient value list require reserved areas of memory in the DSP for storing data values and coefficients. The DSP抯 enhanced Harvard architecture lets programmers store data in Program Memory as well as in Data Memory, and thus perform two simultaneous memory accesses in every cycle from the DSP抯 internal SRAM. With Data Memory holding the incoming samples, and Program Memory storing the coefficient values, both a data value and a coefficient value can be fetched in a single cycle for computation. This DSP architecture favors programs that use circular buffering (discussed briefly in Part 2 and later in this installment). The implication is that address pointers need to be initialized only at the beginning of the program, and the circular buffering mechanism ensures that the pointer does not leave the bounds of its assigned memory buffer梐 capability used extensively in the FIR filter code for both input delay line and coefficients. Once the elements of the program have been determined, the next step is to develop the DSP source code to implement the algorithm. DEVELOPING DSP SOFTWARE Software development flow for the ADSP-2100 Family consists of the following steps: architecture description, source-code generation, software validation (debugging), and hardware implementation. Figure 2 shows a typical development cycle. Architecture description: First, the user creates a software description of the hardware system on which the algorithm runs. The system description file includes all available memory in the system and any memory-mapped external peripherals. Below is an example of this process using the ADSP-2181 EZ-Kit Lite. Source-code generation: Moving from theory into practice, this step梬here an algorithmic idea is turned into code that runs on the DSP梚s often the most time-consuming step in the process. There are several ways to generate source code. Some programmers prefer to code their algorithms in a high-level language such as C; others prefer to use the processor抯 native assembly language. Implementations in C may be faster for the programmer to develop, but compiled DSP code lacks efficiency by not taking full advantage of a processor抯 architecture. Assembly code, by taking full advantage of a processor抯 design, yiELDs highly efficient implementations. But the programmer needs to become familiar with the processor抯 native assembly language. Most effective is combining C for high-level program-control functions and assembly code for the time-critical, math-intensive portions of the system. In any case, the programmer must be aware of the processor抯 system constraints and peripheral specifics. The FIR filter system example in this article uses the native assembly language of the ADSP-2100 Family. Software validation ("debugging"): This phase tests the results of code generation梪sing a software tool known as a simulator? to check the logical flow of the program and verify that an algorithm is performing as intended. The simulator is a model of the DSP processor that a) provides visibility into all memory locations and processor registers, b) allows the user to run the DSP code either continuously or one instruction at a time, and c) can simulate external devices feeding data to the processor. Hardware implementation: Here the code is run on a real DSP, typically in several phases: a) tryout on an evaluation platform such as EZ-Kit Lite; b) in-circuit emulation, and c) production ROM generation. Tryout provides a quick go/no-go determination of the program抯 operation; this technique is the implementation method used in this article. In-circuit emulation monitors software debug in the system, where a tool such as an EZ-ICE?controls processor operation on the target platform. After all debug is complete, a boot ROM of the final code can be generated; it serves as the final production implementation. WORKING WITH THE ADSP-2181 EZ-KIT LITE Our example of the development cycle walks through the process, using the ADSP-2181 EZ-Kit Lite (development package ADDS-21xx- EZLITE) as the target hardware for the filter algorithm. The EZ-Kit Lite, a low-cost demonstration and development platform, consists of a 33-MHz ADSP-2181 processor, an AD1847 stereo audio codec, and a socketed EPROM, which contains monitor code for downloading new algorithms to the DSP through an RS-232 connection (Figure 3). To complete the architecture description phase, one needs to know the memory and memory-mapped peripherals that the DSP has available to it. Programmers store this information in a system-description file so that the development tools software can produce appropriate code for the target system. The EZ-Kit Lite needs no memory external to the DSP, because available memory on-Chip consists of the 16,384 locations of the ADSP-2181抯 Program Memory (PM) SRAM, and 16,352 locations of Data Memory (DM) SRAM. (32 DM locations used for system control registers are not available for working code). More information on the ADSP-2181, the EZ-Kit Lite抯 architecture, and related topics, can be found in texts mentioned at the end of this article. Available system resources information is recorded in a system description file for use by the ADSP-2100 Family development tools. A system description file has a .SYS extension. The following list shows a system description file [EZKIT_LT.SYS]: The listing declares 16,384 locations of PM as RAM, starting at address 0, to let both code segments and data values be placed there. Also declared are 16,352 available locations of data memory as RAM, starting at address 0. Because these processors use a Harvard architecture with two distinct memory spaces, PM address 0 is distinct from DM address 0. The ADSP-2181 EZ-Kit Lite抯 codec is connected to the DSP using a serial port, which is not declared in the system description file. To make the system description file available to other software tools, the System Builder utility, BLD21, converts the .SYS file into an architecture, or .ACH, file. The output of the System Builder is a file named EZKIT_LT.ACH. After writing the code, the next step is to generate an executable file, i.e., turn the code into instructions that the DSP can execute. First one assembles the DSP code. This converts the program file into a format that the other development tools can process. Assembling also checks the code for syntax errors. Next, one links the code to generate the DSP executable, using the available memory that is declared in the architecture file. The Linker fits all of the code and data from the source code into the memory space; the output is a DSP executable file, which can be downloaded to the EZ-Kit Lite board. GENERATING FILTER CODE Part 2 of this series [Analog Dialogue 31-2, page 14, Figure 6] introduced a small assembly code listing for an FIR filter. Here, that code is augmented to incorporate some EZ-Kit Lite-specific features, specifically codec initialization and data I/O. The core filter-algorithm elements (multiply-accumulates, data addressing using circular buffers for both data and coefficients, and reliance on the efficiency of the zero-overhead loop) do not change. The incoming data will be sampled using the on-board AD1847 codec, which has programmable sampling rate, input gain, output attenuation, input selection, and input mixing. Its programmable nature makes the system flexible, but it also adds a task of programming to initialize it for the DSP system. ACCESSING DATA For this example, a series of control words to the codec梩o be defined at the beginning of the program in the first section of the listing梬ill initialize it for an 8-kHz sampling rate, with moderate gain values on each of the input channels. Since the AD1847 is programmable, users would typically reuse interface and initialization code segments, changing only the specific register values for different applications. This example will add the specific filter segment to an existing code segment found in the EZ-Kit Lite software. This interface code declares two areas in memory to be used for data I/ "tx_buf", for data to be transmitted out of the codec, and "rx_buf", where incoming data is received. Each of these memory areas, or buffers, contains three elements, a control or status word, left-channel data, and right-channel data. For each sample period, the DSP will receive from the codec a status word, left channel data, and right channel data. On every sample period, the DSP must supply to the codec a transmit control word, left channel data, and right channel data. In this application, the control information sent to the codec will not be altered, so the first word in the transmit data buffer will be left as is. We will assume that the source is a monophonic microphone, using the right channel (no concern about left-channel input data). Using the I/O shell program found in the EZ-Kit Lite software, we need only be involved with the section of code labeled "input_samples". This section of code is accessed when new data is received from the codec ready to be processed. If only the right channel data is required, we need to read the data located in data memory at location rx_buf + 2, and place it in a data register to be FED into the filter program. The data arriving from the codec needs to be fed into the filter algorithm via the input delay line, using the circular buffering capability of the ADSP-2181. The length of the input delay line is determined by the number of coefficients used for the filter. Because the data buffer is circular, the oldest data value in the buffer will be wherever the pointer is pointing after the last filter access (Figure 4) . Likewise the coefficients, always accessed in the same order every time through the filter, are placed in a circular buffer in Program Memory. Algorithm Code The ADSP-2181抯 MAC stores the result in a 40-bit register (32 bits for the product of 2 16-bit words, and 8 bits to allow the sum to expand without overflowing). This allows intermediate filter values to grow and shrink as necessary without corrupting data. The code segment being used is generic (i.e., can be used for any length filters); so the MAC抯 extra output bits allow arbitrary filters with unknown data to be run with little fear of losing data. To implement the FIR filter, the multiply/accumulate operation is repeated for all taps of the filter on each data point. To do this (and be ready for the next data point), the MAC instruction is written in the form of a loop. The ADSP-21xx抯 zero-overhead loop capability allows the MAC instruction to be repeated for a specified number of counts without programming intervention. A counter is set to the number of taps minus one, and the loop mechanism automatically decrements the counter for each loop operation. Setting the loop counter to "taps?" ensures that the data pointers end up in the correct location after execution is finished and allows the final MAC operation to include rounding. As the AD1847 is a 16-bit codec, the MAC with rounding provides a statistically unbiased result rounded to the nearest 16-bit value. This final result is written to the codec. For optimal code execution, every instruction cycle should perform a meaningful mathematical calculation. The ADSP-21xxs accomplish this with multi-function instructions: the processor can perform several functions in the same instruction cycle. For the FIR filter code, each multiply-accumulate (MAC) operation can be performed in parallel with two data accesses, one from Data Memory, one from Program Memory. This capability means that on every loop iteration a MAC operation is being performed. At the same time, the next data value and coefficient are being fetched, and the counter is automatically decremented. All without wasting time maintaining loops. As the filter code is executed for each input data sample, the output of the MAC loop will be written to the output data buffer, tx_buf. Although this program only deals with single-channel input data, the result will be written out to both channels by writing to memory buffer addresses tx_buf+1 and tx_buf+2. The final source code listing is shown on page 15. The filter algorithm itself is listed under "Interrupt service routines". The rest of the code is used for codec and DSP initialization and interrupt service routine definition. Those topics will be explored in future installments of this series. THE EZ-KIT LITE The Windows-based monitor software provided with the EZ-Kit Lite, makes it possible to load an executable file into the ADSP-2181 on the EZ-Kit Lite board. This is accomplished through the pull-down "Loading" menu by selecting "Download user program and Go" (Figure 5). This will download the filter program to the ADSP-2181 and start program execution. REVIEW AND PREVIEW The goal of this article was to outline the steps from an algorithm description to a DSP executable program that could be run on a hardware development platform. Issues introduced include software development flow, architecture description, source-code generation, data I/O, and the EZ-Kit Lite hardware platform. There are many levels of detail associated with each of these topics that this brief article could not do justice to. Further information is available in the references below. The series will continue to build on this application with additional topics. The next article will examine data input/output (I/O) issues in greater detail through the processor interrupt structure, and discuss additional features of the simple filter algorithm. REFERENCESADSP-2100 Family Assembler Tools & Simulator Manual. Consult your local Analog Devices Sales Office. Also see: (Part 1) (Part 2) (Part 4)
/******** Initialize Constants and Variables *****************/
.const taps=127;
.var/dm/circ data[taps];
.var/pm/circ fir_coefs[taps];
.init fir_coefs:
.var/dm/circ output_data[taps];
/******** Interrupt vector table *****************************/
reset_svc: jump start; rti; rti; rti;
/*00: reset */
IRQ2_svc: /*04: IRQ2 */
si=io(0); /* get next sample */
dm(i0,m0)=si; /* store in tap delay line */
jump fir; /* jump to fir filter */
nop; /* nop is placeholder */
irql1_svc: rti; rti; rti; rti; /*08: IRQL1 */
irql0_svc: rti; rti; rti; rti; /*0c: IRQL0 */
sp0tx_svc: rti; rti; rti; rti; /*10: SPORT0 tx */
sp0rx_svc: rti; rti; rti; rti; /*14: SPORT1 rx */
irqe_svc: rti; rti; rti; rti; /*18: IRQE */
bdma_svc: rti; rti; rti; rti; /*1c: BDMA */
sp1tx_svc: rti; rti; rti; rti; /*20: SPORT1 tx or IRQ1 */
sp1rx_svc: rti; rti; rti; rti; /*24: SPORT1 rx or IRQ0 */
timer_svc: rti; rti; rti; rti; /*28: timer */
pwdn_svc: rti; rti; rti; rti; /*2c: power down */
/******* START OF PROGRAM - initialize mask, pointers **********/
start:
/* set up various control registers */
ICNTL=0x07; /* set IRQ2, IRQ1, IRQ0 edge sensitive */
IFC=0xFF; /* clear all pending interrupts */
NOP; /* add nop because of one cycle */
/* synchronization delay of IFC */
SI=0x0000;
DM(0x3FFF)=SI; /* sports not enabled */
/* sport1 set for IRQ1, IRQ0, FI, FO */
IMASK=0x200; /* enable IRQ2 interrupt */
i0=^data; /* index to data buffer */
l0=taps; /* length of data buffer */
m0=1; /* post modify value */
i4=^fir_coefs; /* index to fir_coefs buffer */
l4=taps; /* length of fir_coefs buffer */
m4=1; /* post modify value */
i2=^output_data; /* index to data buffer */
l2=taps; /* length of data buffer */
cntr=taps;
do zero until ce;
dm(i0,m0)=0; /* clear out the tap delay data buffer */
zer dm(i2,m0)=0; /* clear out the output_data buffer */
/**** WAIT for IRQ2 Interrupt - then JUMP to INTERRUPT VECTOR **/
wait: idle; /* wait for IRQ2 interrupt */
jump wait;
/******* FIR FILTER interrupt subroutine ***********************/
fir cntr=taps-1; /* set up loop counter */
mr=0, mx0=dm(i0,m0), my0=pm(i4,m4);
/* fetch data and coefficient */
do fir1loop until ce; /* set up loop */
fir1loop: mr=mr+mx0*my0(ss), mx0=dm(i0,m0), my0=pm(i4,m4);
/* calculations */
/* if not ce jump fir1loop;*/
mr=mr+mx0*my0(rnd); /* round final result to 16-bits */
if mv sat mr; /* if overflow, saturate */
io(1)=mr1; /* send result to DAC */
dm(i2,m0)=mr1;
rti;
/******* END OF PROGRAM *************************************/
.endmod;
Figure 6.An FIR filter in ADSP-2181 assembly language.
The goal of this article has been to provide a link between filter theory and digital filter implementation. On the way, this article covers modeling filters with HLL programs, using DSP architecture, and experimenting with filter software. The issues introduced in this article include:



.system EZ_LITE; /* gives a name to this system */ .adsp2181; /* specifies the processor */ .mmap0; /* specifies that the system boots and that */, /* PM location 0 is in internal memory */ .seg/PM/RAM/ABS=0/code/data int_pm[16384]; .seg/DM/RAM/ABS=0 int_dm[16352]; .endsys; /* ends the description */ 
To operate on the received data, the code section published in the last installment can be used with few modifications. To implement this filter, we need to use the multiply/accumulate (MAC) computational unit and the data address-generators. 
ADSP-2100 Family User抯 Manual. Analog Devices. Free. Circle 4
FIR Filter code listing for EZ-Kit Lite/**************************************************************** hello81.dsp ?template file for 2181 ez-kit lite board** This sample program is organized into the following sections:** Assemble time constants (system.h)* Interrupt vector table* ADSP 2181 intialization (init1847.dsp)* ADSP 1847 codec intialization (init1847.dsp)* Interrupt service routines** This program implements a simple 憈alk-through?with the AD1847 codec.* The initialization routines have been put into the init1847.dsp file. This* file contains the interrupt vector table, the main 慸ummy?loop, and the* interrupt service routines for the pushbutton and the serial port 0 receive.* The pushbutton (IRQE) causes the LED on the EZ-Kit board to toggle* with each button press.** Parameters controlling the sampling rate, gains, etc., are contained in the* file init1847.dsp. Serial Port 0 is used to communicate with the AD1847.* The transmit interrupts are used to configure the codec, then they are* dISAbled and the receive interrupts are used to implement the 憈alk-through?* audio.** The definitions for the memory-mapped control registers are contained in* the file: system.h** The application can be built by:** asm21 -c -l -2181 hello81* asm21 -c -l -2181 init1847* ld21 hello81 init1847 -a 2181 -e hello81 -g -x***********************************************************/.module/RAM/ABS=0 EzHello;#include
So far, this series has introduced the following topics:
Now, we look more closely at DSP programming concerns that are unique to real-time systems. This article focuses on how to develop algorithms for DSP systems with a variety of I/O interfaces.
What does "real-time" mean? In an analog system, every task is performed in "real time" with continuous signals and processing. In a digital signal-processing (DSP) system, signals are represented with sets of samples, i.e., values at discrete points in time. Thus the time for processing a given number of samples in a DSP system can have an arbitrary interpretation in "real time", depending on the sampling rate. The first article in this series introduces the concept of sampling and the Nyquist criterion--that in real-time applications, the sampling frequency must be at least twice the frequency of the highest frequency component of interest in the (analog) signal (Nyquist rate). The time between samples is referred to as the sampling interval. To consider a system as operating in "real time," all processing of a given set of data (one or more samples, depending on the algorithm) must be completed before new data arrives.
This definition of real time implies that, for a processor operating at a given clock rate, the speed and quantity of the input data determines how much processing can be applied to the data without falling behind the data stream. The idea of having a limited amount of time with which to handle data may seem odd to analog designers because this concept does not have a parallel in analog systems. In analog systems, signals are processed continuously. The only penalty in a slow system is limited frequency response. By comparison, digital systems process parts of the signal, enough for very accurate approximations, but only within a limited block of time. Figure 1 shows a comparison. Real-time DSP can be limited by the amount of data or type of processing that can be completed within the algorithm's time budget. For example, a given DSP processor handling data values sampled at, say, 48-kHz (audio signals), has less time to process those data values, including execution of all necessary tasks, than one sampling 8-kHz voice-band data.
In the filter example described earlier in this series, the input sampling rate is 8 kHz. For the DSP in the example to keep up with real-time data, all processing has to be done within a time budget of 1/(8 kHz), or 125 祍. On a 33-MHz digital signal-processor (30ens per cycle), the time budget provides 125 祍/30 ns, or 4166 instruction cycles, to complete processing and any other required tasks.
Since there is a finite amount of time that can be budgeted to perform any given algorithm, managing time is a central part of DSP system software design. Time management strategy determines how the processor gets notified about events, influences data handling, and shapes processor communications.
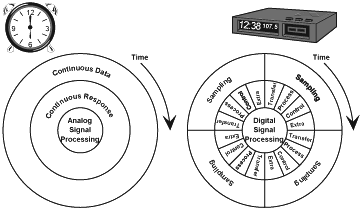
Figure 1. Comparison of analog and digital signal processing. a. Analog: A response value corresponds to each data value at all instants of time. b. Digital: For each sample, the data must be transferred in and processed, an event marks the end of processing (control), and extra time may be necessary for other tasks within the cycle after the designated process occurs.
Event Notification: Interrupts: One can program a DSP to process data using one of several strategies for handling the "event," the arrival of data. A status bit or flag pin could be read periodically to determine whether new data is available. But--"polling" wastes processor cycles. The data may arrive just after the last poll, but it can't make its presence known until the next poll. This makes it difficult to develop real-time systems.
The second strategy is for the data to interrupt the processor on arrival. Using interrupts to notify the processor is efficient, though not as easy to program; clock cycles can be wasted during the wait for an interrupt. Nevertheless, event-driven interrupt programming being well-suited to processing real-world signals promptly, most DSPs are designed to deal efficiently with them. In fact, they are designed to respond very quickly to interrupts. The ADSP-2181's response time to an interrupt is about three processor cycles; i.e., within 75 ns the DSP has stopped doing what it was doing and is handling the interrupt event (vector).
In many DSP-based systems, the interrupt rates, based on the input data sampling rate, are often totally unrelated to the DSP's clock rate. In the FIR example seen earlier in this series, the processor is interrupted at 125-祍 intervals to receive new data.
Interrupt Handling and Interrupt Vectors: Because interrupt processing is such a vital element in DSP systems, processors typically have built-in hardware mechanisms to handle interrupts efficiently. Hard-wired mechanisms are more efficacious than software alone because a DSP's interrupt service routines (ISRs) may have to meet all of the following demands:
On Analog Devices DSPs, fast context switching is accomplished using two sets of data registers. Only one set is active at a time, containing all the data in process during that context. When servicing an interrupt, the computer can switch from the active to the alternate set without having to temporarily save the data in memory. This facilitates rapid switching between tasks.
To handle multiple interrupts, Analog Devices DSPs record their state for each one. Processor state information is kept on a set of status "stacks" located in the DSP's Program Sequencer. A "stack" consists of a set of hardware registers. Current status information is "pushed" onto the stack when an event occurs. This stack mechanism also allows interrupts to be nested; one with higher priority can interrupt one with lower priority.
Two hardware features, interrupt latch and automated I/O, let Analog Devices DSPs stay abreast of the "real world" while processing an interrupt. The latch keeps the DSP from missing important events while servicing an interrupt. The other feature, comprising various forms of automated I/O (including serial ports, DMA, autobuffering, etc.) lets external devices pump data into the DSP's memory without requiring intervention from the DSP. So no data is missed while the DSP is "busy."
When an interrupt request is generated, by an external source or an internal resource, the DSP processor automatically stores its current state of operation, and prepares to execute the interrupt routine. Interrupt routines are dispatched from an interrupt vector table. An interrupt vector table is an area in Program Memory with instruction addresses assigned to particular DSP interrupt functions. For example, in the table below, a Transmit (Tx) interrupt at serial port 1 (SPORT1) of an ADSP-2181 processor will cause the next instruction to be executed at program memory (PM) location 0x0020, followed by the contents of the next three locations, through 0x0023 (the interrupt routine). As the 12 items in the table indicate, an ADSP-2181 can handle interrupts from 11 locations (external hardware, DMA ports, and the serial ports) and the processor Reset. The table lists the programmed instructions assigned to each interrupt vector source in memory locations 0x0000 to 0x002F for an FIR filter program.
Jump start; nop; nop; nop; /* PM(0x0000-03): Reset vector */rti; nop; nop; nop; /* PM(0x0004-07): IRQ2 vector */rti; nop; nop; nop; /* PM(0x0008-0B): IRQL1 vector */rti; nop; nop; nop; /* PM(0x000C-0F): IRQL0 vector */ar = dm(stat_flag); ar = pass ar; if eq_rti; jump next_cmd; /* PM(0x0010-13): SPORT0 Tx vector */jump input_samples; nop; nop; nop; /* PM(0x0014-17): SPORT0 Rx vector */jump irqe; nop; nop; nop; /* PM(0x0018-1B): IRQE vector */rti; nop; nop; nop; /* PM(0x001C-1F): BDMA vector */rti; nop; nop; nop; /* PM(0x0020-23): SPORT1 Tx vector */rti; nop; nop; nop; /* PM(0x0024-27): SPORT1 Rx vector */rti; nop; nop; nop; /* PM(0x0028-2B): Timer vector */rti; nop; nop; nop; /* PM(0x002C-2F): Powerdown vector */
Each interrupt vector has four instruction locations. Typically, these instructions will cause the processor to jump to another area of memory in order to process the data, as is shown in the Reset (at 0x0000), SPORT0 Rx (0x0014), and IRQE (0x0018) interrupt vectors. If there are just a few steps--such as reading a value, checking status, or loading memory--that can be done within the four available instruction locations, they are programmed directly, as shown in the SPORT0 Tx vector (0x0010-13). Any unused interrupt vectors call for return from interrupt (rti), with three nop (no operation) instructions.
The nop instructions serve as place holders--instruction space used to ensure that the correct interrupt action lines up with the hardware-specified interrupt vector. The rti instruction at the beginning of each unused vector location is both placeholder and safety valve. If an unused interrupt is mistakenly unmasked or inadvertently triggered, "rti" causes a return to normal execution.
Data I/O
In DSP systems, interrupts are typically generated by the arrival of data or the requirement to provide new output data. Interrupts may occur with each sample, or they may occur after a frame of data has been collected. The differences greatly influence how the DSP algorithm deals with data.
For algorithms that operate on a sample-by-sample basis, DSP software may be required to handle each incoming and outgoing data value. Each DSP serial port incorporates two data I/O registers, a receive register (Rx), and a transmit register (Tx). When a serial word is received, the port will typically generate a Receive interrupt. The processor stops what it is doing, begins executing code at the interrupt vector location, reads the incoming value from the Rx register into a processor data register, and either operates on that data value or returns to its background task. In the table above, the computer jumps to a program segment, "input_samples", performs whatever instructions are programmed in that segment, and returns from the interrupt, either directly or via a return to the interrupt vector.
To transmit data, the serial port can generate a Transmit interrupt, indicating that new data can be written to the SPORT Tx register. The DSP can then begin code execution at the SPORT Tx interrupt vector and typically transfer a value from a data register to the SPORT Tx register. If data input and output are controlled by the same sampling clock, only one interrupt is necessary. For example, if a program segment is initiated by Receive interrupt timing, new data would be read during the interrupt routine; then either the previously computed result, which is being held in a register, would be transmitted, or a new result would be computed and immediately transmitted--as the final step of the interrupt routine.
All of these mechanisms help a DSP to approach the ability to emulate what an analog system does naturally--continuously process data in real time--but with digital precision and flexibility. In addition, in an efficiently programmed digital system, spare processor cycles left between processing data sets can be used to handle other tasks.
Programming Considerations
In a "real-time" system, processing speed is of the essence. By using SPORT autobuffering, no time is lost to data I/O. Instead, the data management goal is to make sure that the selected address points to the new data.
In the FIR filter example (Analog Dialogue 31-3, page 15), a SPORT Receive interrupt request is generated when the input autobuffer is full, meaning that the DSP has received three data words: status, left channel data, and right channel data. Since this simplified application uses single-channel data, only the data value that resides at location rx_buf+1 is used by the algorithm.
Filter Algorithm Expansion In other applications, the data handling can be more involved. For example, if the FIR filter of the example were expanded to a two-channel implementation, the core DSP algorithm code would not have to change. The code relating to data handling, however, would have to be modified to account for a second data stream and a second set of coefficients.
In the filter code, two new buffers in memory would be required to handle both the additional data stream and the additional set of coefficients. The core filter loop may be isolated as a separate "callable" function. This technique lets the same code be used, regardless of the input data values. Benefits of this programming style include readable code, re-usable algorithms, and reduced code size. If a modular approach is not taken, the filter loop would have to be repeated, using additional DSP memory space.
The SPORT Receive interrupt routine would then consist of the setting of pointer and calling the filter. The revised filter routine is shown in the following listing:
Filter: cntr = taps - 1;mr = 0, mx0 = dm(i2,m1), my0 = pm(i5,m5); /* clear accumulator, get first data and coefficient value */do filt_loop until ce; /* set-up zero-overhead loop */filt_loop: mr = mr + mx0*my0(ss), mx0 = dm(i2,m1),my0 = pm(i5,m5); /* MAC and two data fetches */mr = mr + mx0 * my0 (rnd); /* final multiply, round to 16-bit result */if mv sat mr; / * check for overflow*/rts; /* return */
It's important to note that the only modifications to the core filter loop were the addition of a label, "Filter:" at the beginning of the routine, and the addition of an "rts" (return from subroutine) instruction at the end. These additions change filter code from a stand-alone routine into a subroutine that can be called from other routines. No longer a single-purpose routine, it has become a re-usable, callable subroutine.
With the core filter set up as a callable subroutine, the two-channel data handling requirements can now be addressed. To simplify some of the programming issues, this example assumes that both the left and right channels use the same filter coefficients.
In the third installment of this series, the entire filter application assembly code was displayed. At the top of the code listing, all of the required memory buffers were declared. To expand the filter application to handle two channels of data, the required new variables and buffers need to be declared. For the incoming data, the buffer declaration,
.var/dm/circ_filt_data[taps]; /* input data buffer */
would need to be replaced with two buffers, declared as
.var/dm/circ_filt1_data[taps]; /* left channel input data buffer */.var/dm/circ_filt2_data[taps]; /* right channel input data buffer */
Because both channels are to have the same filter coefficients applied to them, the data buffers are of equal length.
The filter loop subroutine expects certain data and coefficient values to be accessed using particular address registers. Specifically, address register I2 must point to the oldest data sample, and I5 must point to the proper coefficient value prior to the filter routine being called.
Because the filters for both the left and right channel will be sharing the same memory pointers, there has to be a mechanism for differentiating the two data streams. For the data pointer, I2, two new variables need to be defined, "filter1_ptr" and "filter2_ptr."
These locations in memory are going to be used to store address values appropriate for each data stream. The circular buffering capability of the ADSP-2181 is used to ensure that the data pointer is always in the correct place in the buffer whenever the filter is executed. Because the subroutine is now dealing with two buffers, the pointer locations need to be saved when processing for each channel is completed.
To set up the pointers, two variables in data memory need to be declared as follows:
.var/dm filter1_ptr; /* data pointer for left channel data */.var/dm filter2_ptr; /* data pointer for right channel data */
These variable then need to be initialized with the starting address
of each of the data buffers;
.init filter1_ptr: ^filt1_data; /* initialize starting point, left channel */.init filter2_ptr: ^filt2_data; /* initialize starting point, right channel */
The DSP assembler software recognizes the symbol "^" to mean "address of." The DSP linker software fills in the appropriate address value. In this way, the pointer variables in the executable program are initialized with the starting addresses of the appropriate memory buffers.
The following listing shows how the FIR Filter interrupt routine uses these new memory elements. The original Filter subroutine from the 3rd installment has been modified to provide two separate channels of filtering. Instead of launching directly into the filter calculation, the routine must first load the appropriate data pointer. The filter routine is then called, and the resulting output is placed in the correct location for transmission.
/*--------------------FIR Filter--------------------*/input_samples: ena sec_reg; /* use shadow register bank *//* set up for filter 1 */i2 = dm(filter1_ptr); /* set data pointer for filter 1 */ax0 = dm(rx_buf + 1); /* read left channel data */dm(i2,m1) = ax0; /* write new data into delay line, pointer now pointing to oldest data */call filter; /* perform the first filter for left channel data */dm(tx_buf+1) = mr1; /* write left-channel output data */dm(filter1_ptr) = i2; /* save updated filter1 data pointer *//* set up for filter 2 */i2 = dm(filter2_ptr); /* set data pointer for filter 2 */ax0 = dm(rx_buf + 2); /* read right channel data */dm(i2,m1) = ax0; /* write new data into delay line, pointer now pointing to oldest data */call filter; /* perform the filter again for the right channel data */dm(tx_buf+2) = mr1; /* write right channel output data */dm(filter2_ptr) = i2; /* save updated filter2 data pointer */rti; /* return from interrupt */
Because the core filter algorithm no longer handles data I/O, this subroutine can be expanded to more channels of filtering by merely adding more pointer variables and declaring more buffer space (as long as sufficient memory exists!) Similarly, different coefficients can be used for the two filters by setting up variables that contain coefficient-buffer pointer information. In either case, the filter algorithm does not need to be altered. By using this style of modular programming, the user can build up a library of callable DSP functions. Differences for particular systems can thus be reduced to data-handling issues rather than the development of new algorithms. While this programming style does not necessarily allow the algorithm to perform its task more quickly, the system designer has more flexibility in establishing how data flows through the system.
Real-Time Interface Issues: So far, we have examined how real-time programming in embedded systems relies on rapid interrupt response, efficient data handling, and fast program execution. In addition, the flow of data into and out of the processor also influences how well the system will work in a real-time embedded environment.
The primary data flows into and out of a digital signal processor can be both parallel and serial. Parallel transfers are typically at least as wide as the native data word of the processor's architecture (16 bits for an ADSP-2100 Family processor, 32 bits for the SHARC®). Parallel transfers occur via the external memory bus or external host interface bus of the processor. Serial data transfers require considerably fewer interconnections; they are frequently used to communicate with data converters.
Serial Interface: Ease of hardware interfacing is an important element of efficient DSP system implementation. The ADSP-2181 EZ-Kit Lite system uses an AD1847 serial codec (COder/DECoder). Serial codecs permit data transfers via a serial port (SPORT) on the DSP. This serial port is not an RS-232 PC-style asynchronous serial port; it is a 5-wire synchronous interface that passes bit-clock, Receive-data, Transmit-data, and frame-synchronization signals. Major benefits of serial interfaces are low pin count and ease of hardware hookup. The AD1847 requires only 4 signals to interface to the DSP: serial clock, Receive data, Transmit data, and Receive frame-synchronization signal. The serial data stream is time-division multiplexed (TDM), meaning that the same physical line can carry more than one type of information in serial order. In the case of the AD1847 application on EZ-Kit Lite, initiated in the last issue, the serial line carries both left- and right-channel audio information, along with codec control and status information.
| As noted earlier, the processor has various means for handling this data. SPORT Interrupts are generated automatically by the serial port hardware for either Receive or Transmit data and for either a single word or a block of words (Figure 2). | 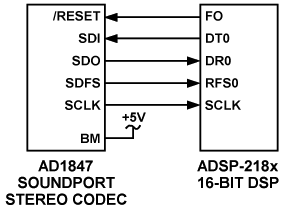 |
| Figure 2. Serial interfacing between digital signal processor and I/O device. |
Parallel Interface: Even with a serial bit clock running as fast as the DSP processor, a serial interface trades data transfer speed for simplicity of wiring, transferring a data word at a fraction of the DSP processor speed. For system performance that requires higher data rates, a parallel interface can be used. When interfacing in parallel, the DSP exercises its external data and address busses to read or write data to a peripheral device. On the ADSP-2181, the buses can interface with up to 16 bits of data.
Parallel data transfer is always faster than serial transfers. The DSP can perform an external access every processor cycle, but this requires really fast parallel peripherals that can keep up with it, such as fast SRAM chips. Parallel data transfers with other entities usually occur at less than one per processor cycle.
| Interrupt handling is different for the serial and parallel interfaces. Since the external data bus of the DSP processor is a general-purpose entity handling all sorts of data, it does not have dedicated signal lines for interrupt generation and control; however, other DSP resources are available. On the ADSP-2181, several external hardware interrupt lines, such as the one for I/O memory select, are available for triggering by an external device, such as an A/D converter or codec. Such an interface is shown in Figure 3, involving a parallel device and the ADSP-2181 DSP. | 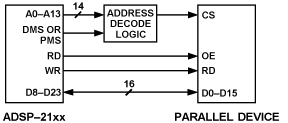 |
| Figure 3. Parallel I/O interfacing for a DSP. |
When responding to the interrupt for parallel data, the processor reads the appropriate source and typically places that data value in memory, by executing instructions similar to those shown here:
irq2_svc: ax0 = IO(ad_converter); dm(i2,m1) = ax0; rti;
"ad_converter" is a previously defined address in I/O space.
REVIEW AND PREVIEW
The goal of this article has been to detail the programming concerns that DSP developers face when handling I/O and other events in real-time systems. Issues introduced include real-time data (samples and frames), interrupts and interrupt-handling, automated I/O, and generalizing routines to make callable subroutines. This brief article could not do justice to the many levels of detail associated with each of these topics. Further information is available in the references below. Future topics in this series will continue to build on this application. The next article will add more features to our growing example program and describe software validation (i.e., debugging) techniques.