图 4 所示的设计按照参考资料 1 的思路，共分为三级。Q 值最高的一级放在第一级，增益最低；中间一级 Q 值略低，增益略比第一级大；最后一级 Q 值最低，增益最大。可见从左到右 Fo 逐渐减小，增益逐渐变大。

图 4. 此增益和 Q 值分配更为接近带宽和压摆率要求

　　另外，我们也可以采用更为常见的方式来设计，将第一级的增益设置为最大，逐级递减。一般来说，这样可以提供更低的输入参考噪声。这对低频率来说是可行的，但不会像想象的那样对整体输出噪声产生太大影响。图 5 所示为同样的滤波器标准，三级增益分别按 5、2、1 排序，实现了相同的整体滤波器形态。同时 Q 值和 Fo 排序从输入到输出也呈现出由高到低的态势。

图 5. 使用更常见的设计流程的增益和 Q 值分配

　　使用生成上面曲线的算法，我们可以把估算的最低放大器带宽乘以该级增益，得到每一级所需的增益带宽积，并制成表格。虽然这种算法只在参考资料 1 中有所提及，但大多数设计工具有类似的 通过Fo、Q 值和增益得到所需的放大器带宽的计算，因此得出的结果也是类似的。我们还可以计算出每一级所需的压摆率峰值。具体计算将在后文介绍。我们这里的目标是实现 4Vpp 的最终输出摆幅，通过综合每一级输出的标称摆幅和 Q 值较高级的过冲阶跃响应导致的 增大了的dV/dT 峰值，我们可以估算出所需的压摆率峰值。

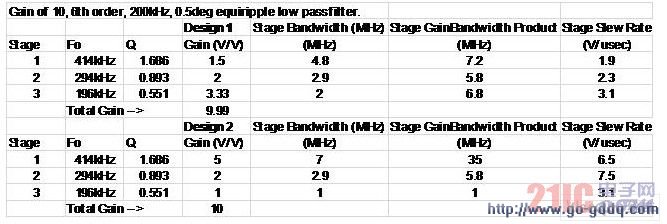
　　上述表中文字

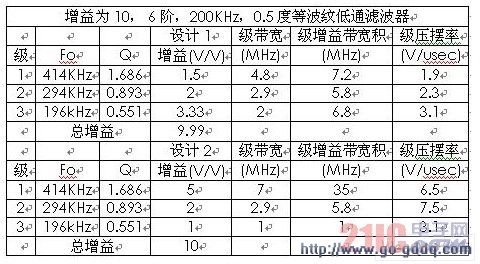
图6. 所需的增益带宽积和压摆率的比较

　　每种方法对带宽的要求体现出值得注意的差异。很明显第二种方法要求的带宽增益积变化较大（35：1，而第一种方法的带宽增益积基本是恒定的）。此外，由于现在头两级要求较高的压摆率，与第一种设计相比，参考资料 1 提出的设计流程需要在头两级采用速度较高的器件（图 5），（ISL28191 的 GBP 是 61MHz，ISL28114 的 GBP 是 7.7MHz）。最后一级的压摆率保持不变，但前面两级现在要求更高的压摆率。最终的输出总是在固定的目标输出步长和滤波器整体形态下达到相同的压摆率，不过第一种设计在前两级要求较低的峰值压摆率，这在每一级都使用同样的放大器的情况下，是更加受欢迎的。

　　虽然可能找到某种“优化”算法来实现准确的增益分配，以得到固定的增益带宽标准，但以本文所述的大略的方法来分配增益可以便于归集所需的放大器带宽。出于多种原因，在滤波器级数超过一级的情况下，高 Q 值的级增益应保持较低，而如果需要更为一致、适中的放大器带宽标准，应更多地将总增益分配到较低Q 值的级上。这样还会得到较低的 Q 值随 Ko 变化的灵敏度。

　　但是如果把设计 1 中的 Q 值从输入到输出由高到低排序会怎么样呢？这样确实看起来更能保持各级所需压摆率的一致性，另外还可以在削波和整体噪声方面体现出优势。

　　二阶阶跃响应所需的压摆率峰值计算

　　多级有源滤波器的每一级都会产生输出电压转换，这就要求限制最大 dV/dT。在这个由阶跃响应主导的例子中，如果该 dV/dT 超过了选定的运算放大器的额定压摆率，阶跃响应通常会大幅偏离预期值。因此，在谨慎的增益和 Q 值排序方法中，我们需要考虑内部和输出级对 dV/dt 峰值的隐含要求。频域主导的应用会对每一级输出都有隐含的压摆率要求。在这种情况下，以总体响应的 SFDR来作为 标准会更加有意义，但这方面的讨论已经超出了本文的范围，不过可以得出与本例使用的阶跃响应主导的分析类似的结论。

　　虽然多级有源滤波器内部实际的波形在时域上可以非常复杂，但可以采用合理的保守方法，把每一级当成受到了理想的输入阶跃激励来分析。任何真实的滤波器产生的级间输入的边缘速率都会低于理想阶跃，这样就给我们一些设计裕量，并允许使用较为简单的等式。

　　如果我们假定任一二阶低通滤波器级受到理想输入阶跃激励后会产生 Vopp 的目标摆幅，我们就可以通过分析输出时间波形得出 dV/dt 峰值。有意思的是，其结果在文献中很难找到，不过从参考资料 4（等式 55），我们可以得到一个简单的近似等式，如等式 1 所示。

等式 1

　　如果我们知道理想的输出端完整步长以及第二级的 F-3db，这个近似等式可以帮助我们很方便地得出 dV/dt 峰值。我们可以通过下面的式子从目标滤波器极点得到F-3dB

　等式 2

　　根据设计 1 和设计 2 所举的例子，每一级 F-3db 的值计算如表 1 所示。（记住我们保持 Q 值和 Fo 排序不变，只是简单地分配了不同的增益，使滤波器内部的阶跃幅度不同）

表 1.

　　那么我们再来观察 Q 值最高的一级，这一级通常也有最高的 Fo，也就是最大的带宽。如果我们能够推测出固定的最大输出 Vpp 标准，就可以让等式 1 的结果落在更小的范围内。最简单的方法是随 F-3db 带宽的增加，降低所需的 VSTep。设计 1 实际上就是通过在输入级使用更低的增益做到了这一点。而设计 2 显示了没有降低较高 Q 值级（图 6）所需的 Vstep  得到的压摆率结果（如图 6 所示）。图 6 显示的设计 1 和设计 2 的压摆率是以 4Vpp 的最终输出目标摆幅为条件得出的。具体是使用等式 1 计算出该输出条件下的压摆率（使用 2 倍乘数以得到额外裕量），然后用该级标称摆幅除以该级标称增益得出由前一级进入最后一级的步长，最后使用该摆幅和该级的 F-3db 计算所需的压摆率，依次类推回第一级。

　　每个 Q 值较高的级都会在阶跃响应中产生相当大的过冲。设计 1 通过让有较高过冲的级的摆幅较低，并从输入到输出逐步增大阶跃摆幅来避免削波。设计 1 的阶跃响应仿真运行结果（参考资料 1）得出的阶跃响应如图 7 所示。该图展示了通过滤波器每一级的输入和输出电压。注意摆幅的逐渐增大和最终输出级极低的过冲。这是这种类型滤波器形态的典型特征。其在 +/-2.5V 双极电源下产生 +/-2V 双极性摆幅。

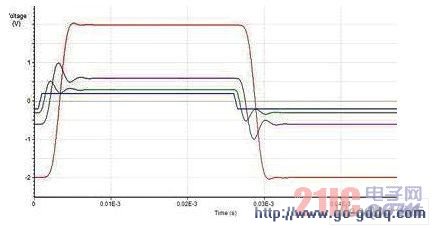
图 7. 设计 1 的阶跃响应仿真

　　相比之下，设计 2 的阶跃响应在级间出现了削波，导致非常不理想的仿真响应结果。这是因为第一级的增益较大导致设计中较早出现了大摆幅。如图 8 所示，仿真中宏模型正确的预计到第二级的输出会出现削波，而最后一级将其干净地滤除了。

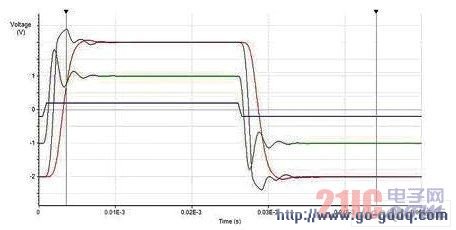
图 8. 设计 2 的阶跃响应出现削波

　　这明显比设计 1 的效果差。虽然这是个有些极端的例子，但这也确实说明了用最后一级增益来降低级间削波风险的重要意义。

上一页  [1] [2] [3]  下一页