多级滤波器 Q 值排序对噪声增益峰值的考虑

　　对曾经测量过 SKF 滤波器输出噪声频谱的人来说，都会有些惊讶地发现噪音峰值有多么高。SKF 滤波器的一项最不为人注意的特性是其高峰值噪声增益在某种程度上可以通过认真选择电阻值来减轻。

　　运算放大器线路的“噪声增益”指输出电压的分压比与差分输入电压比值的倒数。这也给出了运算放大器自身的输入噪声电压到输出端的增益的频率响应。同样它还是运算放大器开环增益与该噪声增益的比，即 SKF 滤波器内部通带频率上的环路增益。这是极为有用的因子，它说明环路增益越大，谐波失真越低。因此，出于多种原因考虑，应了解并尽力降低 SKF 的噪声增益峰值。

　　等式 3 所示的是图 1 二阶低通 SKF 滤波器的噪声增益拉普拉斯传递函数的基本形式。分子是一个二次多项式，实数零点分布在较宽的范围内（一个小于 ω0，一个大于 ω0），而分母的极点是滤波器需要的极点。这个分母的表达式实际上是导入增益元件前的无源2 R和2 C电路的极点等式（将图 1 中的放大器从电路中去除，让 C2 接地，就可以得到 C2 之上的从输入到输出端的传递函数，而这个表达式的极点就是 SKF 噪声增益表达式的分母）。

　　等式 3 噪声增益à

　　分母等式与所需的滤波器响应一致。如果我们在分母的线性系数中用 Ko/R2C2 项来做替代，然后按滤波器指标项重写等式，我们会发现实际上我们在噪声增益响应方面没有多少裕量。

　　等式4  滤波器指标项的噪声增益à

　　除 1/R2C2 极点外，该等式中的每一项都已经被所需的滤波器形态、DC 增益以及 Ko 决定了。这种现象在某种程度上可以用来降低噪声增益峰值，但噪声增益峰值主要还是受控于所需的滤波器 Q 值。简单地说，最好让 SKF 滤波器的 R1/R2 值大致处于 0.15 至 0.7 之间。使该比例尽量接近 0 从数学上来说是准确无误的，这样可以减少噪声增益峰值，但 R1 为 0 又会带来其它问题。

　　所以噪声增益在频率范围内始于 Ko，终于 Ko。在 ω0 附近，由于极点等式反映的所需的滤波器形态（Q >.707 会在所需的频率响应内形成峰值）和低于 ω0 时形成的零点造成的峰值，因此会有较大峰值出现。一个显然的问题是运算放大器环路内的噪声增益峰值是否会影响稳定。在峰值位于放大器开环响应范围内的时候会影响稳定。不过，即便在图 1 和图 2 所示的极低带宽裕量条件下，噪声增益曲线与开环增益的交点也会远高于下面所示的峰值。但是这个问题说明了不要采用太大的放大器带宽与 Fo 乘数。理论上讲，可以使用几乎任何放大器带宽，通过迭代，得到所需滤波器形态要求的电阻值和电容值。不过让放大器带宽与 Fo 的比值过大就会引起局部环路稳定问题。

　　图 9 所举示例显示的是设计 1 第一级的噪声增益幅度。它采用参考资料 1 的设计算法，首先控制 R1+R2 的值使加在运算放大器自身的噪声近乎可以忽略，然后在上面建议的范围内设置 R1/R2 比例。

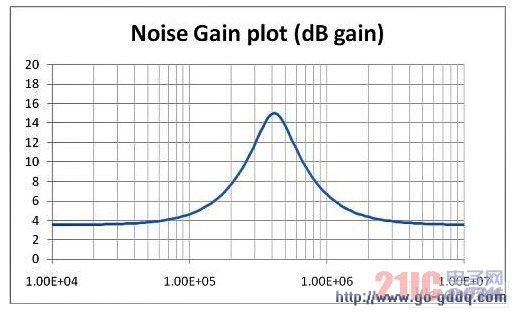
图 9. 设计 1 第一级的噪声增益幅度

　　这里的初始增益是 1.5V/V，最终的噪声增益是 3.56dB。在 414KHz 的 Fo 频率附近，我们发现了峰值惊人，增益增加了近 11.4dB，高达 15dB，是滤波器所需增益的 3.7 倍。这一级所需的滤波器形态只体现出了从 3.56dB 的DC 增益到最大 增益8.44dB 的峰值，远远低于隐藏于该响应中的噪声增益峰值。如果该较高 Q 值级还能提供更多滤波器总增益，整个曲线将会上移。这将在后面演示。

　　谨慎起见，应该在该超高噪声峰值之后安排 Q 值更低、Fo 更低的级。这样可以过滤这些峰值，实现较低的整体输出噪声。

　　图 10 显示的是设计 1 滤波器每一级的输出噪声。它包含了根据参考资料 1 生成的设计的全部参数、噪声电压、噪声电流以及电阻噪声。前两级的输出有明显的噪声峰值，但最终输出噪声峰值近乎可以忽略，因为最后一级的 Q 值较小。这里的噪声峰值在 190KHz 时为 1.76?V/&raDIC;Hz。

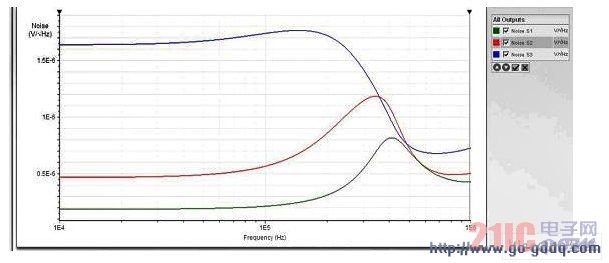
图 10. 设计 1 的输出噪声图

　　让我们回到设计 2，采用 ISL28113 来完成设计，根据下面的噪声图（设计中经设置电阻后会以运算放大器噪声电压为主，故该图主要体现的是运算放大器的电压噪声效果）进行输出噪声的公平比较。该图显示前两级都出现了明显的噪声峰值，但由于最后一级 Fo 和 Q 值相对较低，起到了良好的滤除作用。该图显示 200KHz 时噪声峰值为 1.49?V/&radIC;Hz，略低于设计 1。

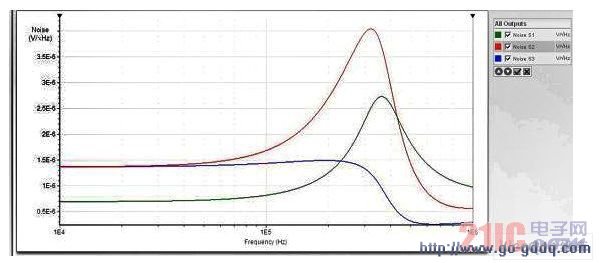
图 11. 设计 2 的输出噪声

　　因此，在这种情况下，把增益更多地放在第一级确实可以轻微降低总输出噪声。但一定要把Q 值最低的一级布置在最后，这一点是非常重要的。把 Q 值最高的级放在后面的设计会导致最高的整体噪声。即便该级的 DC 增益只有 1，其较高的频率峰值也会形成不理想的整体噪声结果。

　　有兴趣的话，还可以计算出两个设计的输出噪声 Vpp。计算的方法是将频率范围内的输出噪声功率相加得到（Vrms）2，然后开方，将平方根乘以 6 就得到大致的噪声 Vpp。图12显示的是如果两个滤波器后接截止频率在x轴上的矩形噪声滤波器的情况下估算测得的输出噪声Vpp。

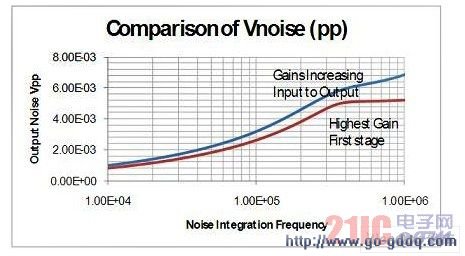
图 12. 设计 1 与设计 2 的综合输出噪声电压比较

　　举例来说，我们在 200KHz 六阶设计后接一个 500KHz 的矩形滤波器，我们可以在设计 2 上测得大约 5mVPP，在设计 1 上测得 6mVPP。总体来说，这点差异不会给设计 1 前边提到的优势在噪声方面造成太大影响。

　　所以在这种情况下，将增益更多地排布到第一级可以带来某些噪声方面的优势。但这里的想法是建议把 Q 值适中、增益适中的级放在第一级，随后是 Q 值最大、增益较低的级，最后是 Q 值最低、增益较高的级。如参考资料 1 所提供的自动设计算法，把 Q 值从高到低排序，把增益从低到高排序，可以在放大器带宽、压摆率一致性、阶跃响应过冲以及削波性能方面实现优异的特性，只是在某些情况下输出噪声有适度的增加。

　　结论

　　如果多级低通有源滤波器的目标之一是在每级使用相同的放大器的同时，降低对运算放大器的设计裕量要求，那么给 Q 值较高的级分配更低的增益是非常合理的选择。为避免最终输出出现噪声峰值，最好把 Q 值最低的级放在最后。为限制级间削波，在滤波器总增益大于 1的情况下，该低Q 值级应具有一定的增益（尽可能大于 2）。增加第一级的增益可以略微减少输出噪声，而将具有低增益的最高 Q 值级放在中间可以略微改善噪声特性。

上一页  [1] [2] [3]