摘要：针对功率型 LED 器件的热特性，以热应力理论为依据，采用有限元软件A NS YS 进行热应力计算，得到了Lumileds 的1 W LED 瞬态温度场和应力场分布云图， 基板 顶面平行于X 轴路径上的热应力、应变及剪应力的分布曲线。模拟结果表明最大应力集中在键合层边角处；轴向最大位移在 透镜 与热沉接触边缘；最大剪应力集中在键合层的边角区域。通过实验测试了LED 基板底面中心点的温度变化，与仿真结果相符合，研究了各层材料导热系数对LED 温度场和应力场分布的影响。最后根据以上的研究结论提出了提高LED 品质的方法。论文结果对 大功率LED 封装具有意义。

　　0 引 言

　　LED 因具有无污染、高效率、寿命长、体积小等优点，成为最有前途的照明 光源 。随着功率型LED在照明领域应用的不断发展，对LED 小型化、高功率化的要求越来越迫切，低热阻、散热良好及低应力的封装结构是功率型LED 器件的技术关键。现有研究结果表明，键合材料对LED 封装热阻影响最大，提高功率型LED 散热能力的关键是减小键合层的热阻。键合材料导热系数较低，固化后材料间的接触热阻很高，导致温度梯度大，将产生很大的热应力；另外，键合材料与 芯片 、热沉间的热膨胀系数（CTE）差异较大，当膨胀受到外部约束时也会产生较大热应力。封装过程产生的热应力不仅影响LED 器件的物理稳定性，还会使封装硅胶透镜的折射率发生改变，从而对LED 的出光效率和光场分布造成影响。热应力大小已成为*价功率型LED 可靠性的主要指标之一。

　　目前，国内外已经对LED 热应力分布做了相关研究。 2006 年，Jianzhen Hu 等人对Ga-N 基LED 热应力分布进行了有限元模拟仿真，结果表明LED 封装的最大热应力集中在芯片和键合层接触地方的边缘处； 2007 年，于新刚等人分析了基板材料导热系数对LED 结温和最大热应力的影响； 2008 年，戴炜峰等人利用有限元模拟了大 功率LED 的瞬态温度场和应力场的变化情况。但上述研究中都将LED 温度场和应力场分别进行了模拟分析，而没有分析温度场对应力场的对应变化关系，也未分析应力与应变的变化趋势，而且从公开的文献来看，并未发现任何有关研究键合层材料这个关键因素对LED 应力场分布的影响。

　　论文以热应力理论为依据，模拟了LED 瞬态温度场和应力场分布的变化，并与实测的LED 基板底部中心温度变化情况进行了对比研究；并分析了瞬态温度场和应力场的对应变化关系；模拟研究了键合层材料导热系数对LED 结温和最大等效应力的影响；计算了基板顶面平行于X 轴路径上热应力、应变及剪应力的变化趋势，论文的研究对LED 的封装热设计具有意义。

　　1 热应力理论模型及物理模型

　　根据传热理论，具有内热源的大功率LED 瞬态温度场分布应该满足如下方程：

　　其中：T 为温度；t 为时间；x, y, z 空间三维坐标系；α 为热膨胀系数，α 满足方程：

　　其中：λ 为导热系数，ρ 为密度，c 为比热容。按照热弹性力学理论，LED 温度梯度导致的热膨胀受到外部约束时产生的瞬态热应力，满足如下方程：

　　式中：σ 为热应力，α 为热膨胀系数，E 为弹性模量，T 为温度，Tref 为参考温度。由式（3）可以看出，LED 内部温度场是确定热应力大小的前提，而温度分布由热传导微分方程（1）决定，只要给出相应的边界条件即可得到温度场及应力场分布。

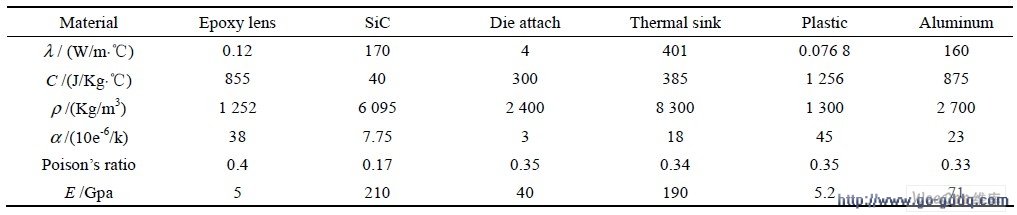
　　以Lumileds 的1 W 功率型LED 器件（如图1）为研究对象，该LED 由透镜、芯片、键合层、热沉、基板及塑封料组成。热量由芯片经键合层传导到热沉，最后由基板与空气进行对流散热。LED 各种封装材料热性能参数如表1 所示。

图1 Lumidleds 1 W LED 模型

表1 LED 封装材料的热力学参数

　　2 实验、仿真结果与分析

　　采用自由网格建立LED 有限元模型，热源和键合层采用一级网格，其余采用六级网格。芯片输入热功率按90%计算为0.9 W，环境温度为25℃，生热率4.0×109 W/m3，在LED 模型与空气接触面加载对流系数为10 W/m2.℃，并忽略各层材料中的接触热阻，设定求解时间为600 s，时间子步为20 s，利用有限元软件ANSYS 求解式（1）~（3）即可得到Lumidleds 1 W LED 瞬态温度场分布。

　　2.1 LED 瞬态温度测试实验与仿真

　　为了验证有限元仿真的可靠性，设计了一组实验对Lumidleds 1 W LED 进行温度测试，测点为 铝基板 底面中心，给定电流350 mA，电压3 V，温度测试时间为10 min，每隔10 s 记录一次数据，实验结果表明点亮8 min 后，LED 基本处于热平衡状态，此时基板中心温度为56℃。仿真结果表明此时LED 结温为76.1℃（如图2 所示）。

　　LED 从开始工作到稳态过程中，基板测点温度变化曲线和仿真结果如图3 所示，升温过程中，实测结果略低于仿真结果，到达稳态后，两则相差2.9℃，验证了有限元分析的可靠性。材料参数的误差、仿真过程中忽略了热辐射以及将对流作为简单边界条件施加是产生误差的主要原因。

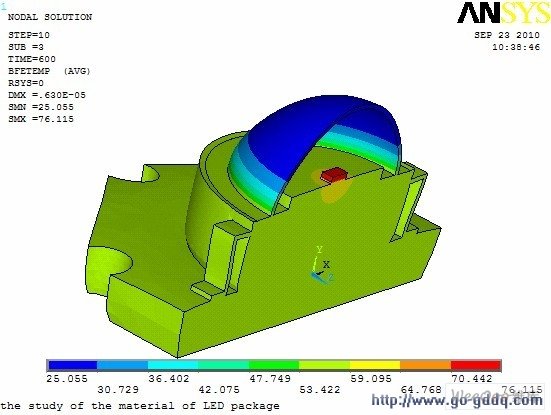
图2 Lumileds 1 W LED 稳态温度场分布云图

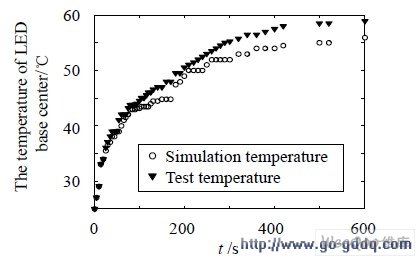
　图3 Lumileds 1W LED 基板中心点温度实测数据与仿真数据对比

　　2.2 LED 热应力与热变形的模拟结果与分析

　　在计算得到瞬态温度场分布后，将热单元solid70 转换为结构单元，用循环命令将每一个时间步的温度场读入到应力场，并在基板底面三个方向加约束，计算得到稳态时应变和应力场如图4（a）、（b）。

　　图4（a）是Lumileds 1 W LED 在最终时刻（600 s）后总位移云图，内部带网格云图表示未变形前的结构，另一个实体云图表示LED 在受热膨胀后的变形效果，这里对变形量按比例进行了放大。由图可见，热变形主要集中在透镜和塑封料处，特别是透镜与塑封料接触地方，最大变形量达到6.3 μm。由于基板底部加了X、Y、Z 三个方向约束，相当于基板底部被固定，因此基板底部位移量为0 μm。

　　图4（b）是LED 在稳态时应力分布云图。由图可见，透镜、外封塑料层和基板顶部的热应力很小，基板底部应力明显大于顶部。这是由于基板底部热膨胀受到X、Y、Z 三个方向的约束所致。图5（a）为基板底部的应力分布图，最大在基板底面的边角处，为163 MPa；图5（b）显示基板顶部最大的热应力在热沉与基板交界处，基板顶部边角处只有1.43 MPa。

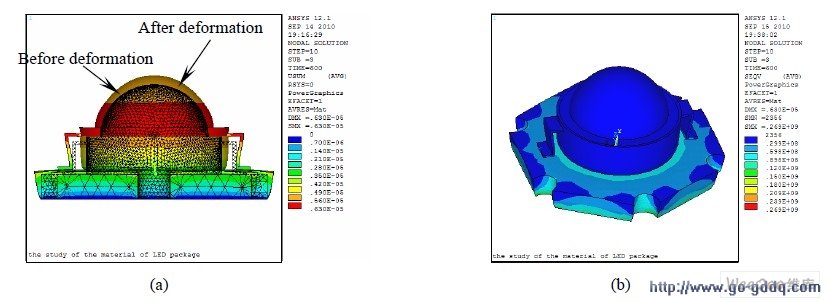
图4 Lumileds 1 W LED 的热变形云图（a）和等效应力云图（b）

　　图6（a）是键合层等效应力分布云图。由图可见，最大热应力在键合层边角处为269 MPa，键合层最小应力也达到94.6 MPa。这是由于键合层导热系数较小，热阻较大，热量在此处积聚较多，导致在键合层边角处热应力成为整个封装器件最集中部分。图6（b）是芯片等效热应力分布云图，芯片最大应力在四个边角处为34.1 MPa，如此高的应力易引起芯片破裂，要特别注意。

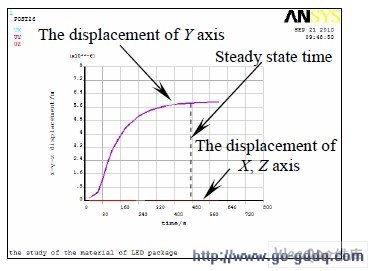
图5 LED 基板底部（a）和顶部（b）的热应力分布图

图6 Lumileds 1 W LED 键合层（a）和芯片（b）的等效热应力分布

　　芯片顶面中心节点的位移随时间变化曲线如图7 所示，X 和Z 方向位移近似为零，Y 方向的位移随着时间和温度场的变化而不断变化（Y 向为器件纵向即温度传递方向），在光源点亮500 s 左右后，温度场进入稳定状态，此时芯片应变量达到最大6.3 μm，与瞬态温度场的变化相符。

　图7 Lumileds 1 W LED 芯片中心节点位移随着时间变化曲线

　　2.3 基板路径上的热应力、应变及剪应力的模拟与分析

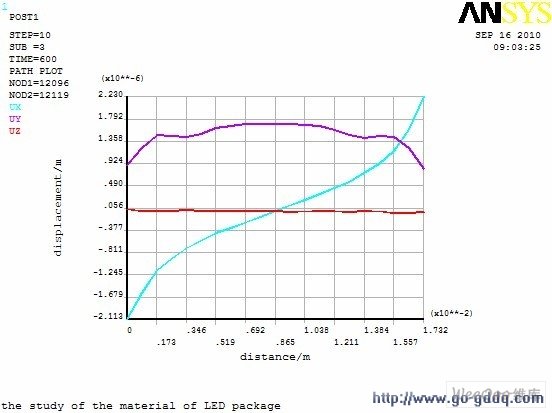
　　在基板顶部平行于X 轴方向上选取如图8 所示的一条轴向路径，考察路径上的应变、应力及剪应力的变化情况。

图8 基板顶面上的路径示意图

　　图9（a）表示的是路径上X、Y、Z 三个方向的位移变化曲线。由图可知，路径上UZ 几乎趋于零，Y 方向上，两端形变较小，中间偏大，这与温度场分布相符合；UX 两端位移较大，往中间逐渐减小，且两端关于中心对称，这与基板的形状与约束条件有关。图9（b）为路径上应力变化曲线，SX 与SZ 方向的应力变化趋势相同，保持较高的应力水平，而SY 一直保持较低应力水平。X、Y、Z 三个方向显示应力值都是两边大于中间，可以看出最大的应力出现在边角处。