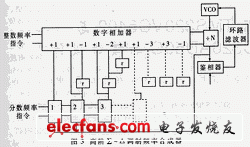
锁相环路由于具高稳定性、优越的跟踪性能及良好的抗干扰性,在频率合成得到了广泛应用。但简单的锁相环路对输出频率、频率分辨经等指标往往不能满足要求,所以要对简单锁相环路加以改进。小数分频锁相环则是改进方案之一。

　　采用小数分频锁相环带来的一个严重问题是分数调制(又称相位调制)问题。

　　产生的原因是：当环中锁定时,分频器的分频比不是固定的,而是在N和N+1之间变化。由于输出频率fo=N·F×fr,所当分频比为N时,鉴相器的fo/N信号相位超前fr的相位,而且两者相位差不断增加,直到分频比为N+1。这时相位差突然降到0,其结果是鉴相器的输出呈现阶梯锯齿波形。这样一个波动电压加到压控振荡器上就会产生频率调制。对于上述由于分频比变化而引起的相位调制通常采用以下模拟补偿措施：将小数累加器的累加和通过D/A变换器变换成补偿电压(其电压大小与鉴相器输出的相位调制电压成正比而极性相反),再加到求和放大器上进行抵消。这种模拟补偿措施有以下不足之处：(1)补偿电路过于复杂,调试不方便;(2)由于补偿电压和相位调制在时间上和幅度上难以达到一致,因此补偿程度有限的,一般存在1%以上的误差。因此,一个全数字的方案被提出来,它很很好地解决分数调制问题,这就是∑-Δ调制。

　　1 ∑-Δ调制频率合成器及其实现

　　∑-Δ调制频率合成器是一个无相位补偿的分数频率合成,用∑-Δ调制器取代普通分数环中的累加器。把所需分频比的分数部分作为∑-Δ调制器的输入,由调制器产生脉冲密度调制信号去控制频率合成器的分频比,以达到分数分频的目的。

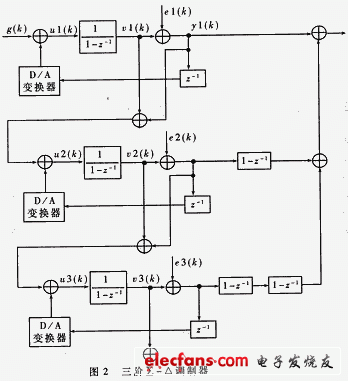
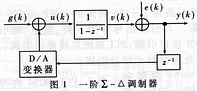
　　具有1位量化器(比较器)的一阶∑-Δ调制器如图1所示。1位D/A变换器完全线性,引入量化噪声e(k),则量化器可作线性化处理,得图1线性化模型,其中k为整数,g(k)为0～1的分数,代表小数分频分频比的小数部分。Y(k)为0或1,分别代表分频比为N和N+1的情况。理论分析表明[1],一阶∑-Δ调制器对信号是全通的,能传递所需信号。引外,它对噪声呈现低频端掏大、高频端抑制小甚至放大特性。这就是∑-Δ调制器的噪声变形特性,它把噪声能量推向高频端,而高频噪声可由环路低通滤波器滤除,因此一阶∑-Δ调制器频率合成器具有较小的噪声。为更好地抑制噪声,可用高阶∑-Δ调制器,它由多个一阶∑-Δ调制器级连而成。级连的方法如图2所示。第一级的量化噪声e1(k)(由v1(k))与y1(k)差得到)e2(k)作为第二级的输入,第二级的量化e2(k)作为第三级的输入,各级输出作如图的处理。调制器的输出用来控制分频化。同阶∑-Δ调制频率合成器电路实现框图如图3.采用多级累加器结构,与小数分频频率合成器比较,∑-Δ调制频率合成器利用3个累加器或更多个累加器代替单个累加器,每个累加器输出与下一个累加器的输入相接。和通常的分数环一样,累加的溢出控制分频比。第一个累加器同分数系统中的累加器以同样的方式工作,它溢出时,在一个周期内,将分频比从N变到N+1。第一个累加器的输出代表相位误差,如不进行其它修正就会产生相位误差。这个输出再次由第二个累加器进行数字积分,由它的输出进一步控制分频比。控制方法如图2所示。第二个累加器的溢出使分频比变为N+1,下一时钟周期变为N-1;第三个累加器将分频比变为N+1,N-2,N+1;第四个累加器将分频比变为N+1,N-3N,N+3,N-1等等。2 ∑-Δ调制器原理设计

　　∑-Δ调制频率合成器采用多级累加器结构,对于一般的使用场合,采用三级累加器已能够满足信号指标的要求。为了与微机接口的方使及频率控制字的换算方便,