CORDIC (Coordinate Rotation Digital Compute)算法广泛应用于正弦函数、余弦函数、向量的旋转、直角坐标、极坐标相互转换等各种函数的计算[1]。这种算法的显著特点是在硬件实现该算法时只需要加法器和移位寄存器，因此在现代通信系统中得到了广泛使用。随着超大规模集成电路的发展，人们对利用硬件实现CORDIC算法进行了深入的研究，提出了一些改进的CORDIC算法[2, 3]。本文针对MVR-CORDIC算法[4]，提出进一步的改进方法，使之更适合于用超大规模集成电路实现。

CORIDC算法
传统CORDIC算法的基本思想是若要求平面矢量进行某一特定角度θ的旋转，则需将此角度值分解，用一组预先规定的基本角度集的线性组合逼近，也即进行多次大小为基本角度集合中对应的角度值的旋转。CORDIC算法是基于

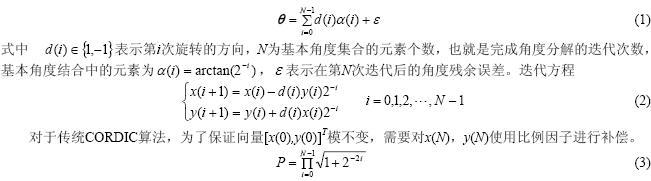
由上式可以看出，传统CORDIC算法的比例因子对于任意的角度分解都是固定的。