最后，还必须注意转换器对功率的贡献。一些转换器可能以丢失内部信息为代价来节省功率损耗，例如接受差动时钟（为了实现更低的噪声/抖动）所需要的参考电压或时钟放大器、诸如 PECL 或 LVDS 的小摆幅时钟电平，或者截平滤波时钟（正弦曲线）。这个问题将在下文进一步阐述。

时钟信号

为了获得最佳的 ADC 性能4，时钟信号是最令人担心的问题。虽然所有的 ADC 都有一个时钟输入端，但其中一些要比另一些更容易使用。最关键的问题是时钟抖动、占空比以及必须的时钟电平，当用高输入频率进行采样时，能够大体上获得较好的性能参数。

为了实现低抖动，用户通常使用带通滤波器过滤时钟信号来达到该目的。这还将产生 50% 的占空比，接近于许多 ADC 的最佳条件。不过，由于该滤波器的插入损耗时钟信号振幅将受到影响，且时钟信号将变成正弦曲线而不是方波。为了接收高质量的时钟信号，TI 和其他一些厂商在 ADC 的输入端添加了时钟放大器。它的作用是将正弦曲线修正成方波并为内部电路的时钟循环提供所需的增益。此外，时钟放大器还提供了差动接口，能够减小时钟信号线路中噪声耦合的影响，从而减小抖动。当然，这是以增加 ADC 的功耗为代价的。

然而，一些 ADC 可能还需要 CMOS 电平的方波时钟信号。这类 ADC 的输入必须是单端口的，而且能够抑制外部噪声源与时钟路径耦合。大部分此类 ADC 是为了对低输入频率（50 MHz 以下）进行采样并且能够获得很好的性能。医学超声波就是此类 ADC 的一种典型应用。不过，用户在更高的输入频率（例如通讯应用中）下为了获得高信噪比（大于 60s），就需要提供外部元件来使时钟信号变成方波，并有效地增大功率与电路板面积。即使有了这些外部元件，用户仍然必须考虑单端接口，而且最终的设计很可能不能获得 ADC 采用内部时钟放大器时所能达到的最优性能。

为了提供一致的产品说明书，TI 在相同时钟条件下的产品说明书中使用了相同的图表与性能参数。对于具有差动输入时钟信号的器件而言，通常采用正弦曲线，虽然它并不是 ADC 的最佳条件（由于时钟边缘压摆率的限制）。为了涵盖转换器所有可能的应用情况，TI 开始在产品说明书中引入了 3D 等高线图表（请参见图 1），这就允许用户可以得到在给定输入与采样频率下的典型性能。我们知道，输入时钟信号的所有条件在试验时都是保持不变的，除非改变采样频率。这意味着如果使用正弦波时钟信号，减小采样频率将会使时钟边缘变慢，从而加剧实际的抖动。这是每个 ADC 普遍存在的现象，4但是 TI 设计的 ADC 能够尽可能地将抖动最小化。虽然这是最坏的情况，而且减小抖动的技术有很多种，但是在实验中改变时钟条件是不公平的；同样的，如果保持时钟条件不变，那么信噪比 SNR 将随着抖动的增加而降低。用户必须要知道，如果没有时钟放大器，性能的降低可能更多。此外，用户还必须要清楚如果能够提供一个抖动很小的方波时钟信号，那么 ADC 的性能就会有很大的提高。

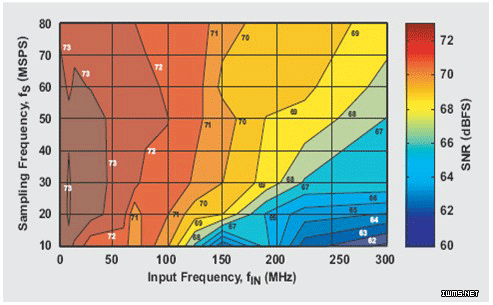
图 1 SNR 与输入和采样频率5的曲线关系

输出时序

为了捕捉传输到 FPGA、ASIC、DDC 或其他跟随 ADC 的逻辑器件的输出数据，用户必须要知道输出数据的窗口是稳定的。不过，重点是大多数厂商均致力于提供一致且完善的产品说明书限制。这是因为用于生产的最终测试结果受一些因素的影响，例如自动测试设备的精度、不能直接访问输出端（数据正在缓冲中）、很难像产品说明书一样设置相同的条件（例如数字负载）等等。为了克服这些局限性，TI 通过设计与特征化（即用统计方法来设置这些参数），当生产中不对设备进行测试时，这能促使我们设置更宽的防护频带。而如果将相同的限制条件用于其他厂商的话，经常会导致不完善或不精确的产品说明书。

设计人员应对没有任何质保书的器件、有质保书但是条件不切实际的器件（例如 0-pF 负载）、没有明确用于捕获数据所需的参数的器件（例如，给出了建立时间但没有给出保持时间）、没有说明规范所使用的 VOH 和 VOL电平的器件（例如，给出从 50% 到 50% 的信息，但是要推导出 VIH/VIL 逻辑电平却很麻烦)、或者没有说明对整个工作温度范围内详细参数的器件进行明确的询问。

此外，为了改进数据捕获窗口，TI 与其他厂商均提供了一款输出时钟，与输入时钟相比该时钟能够更好地跟踪输出数据。使用输出时钟可以减小应用中的时序局限。

最后，请注意，建立与保持时间的定义和门电路建立与保持时间的对应部分相同。在门电路中，建立时间表示数据在门电路输入端准备好的时间比时钟边缘闭锁它的时间提前了多少。时间提前得越多，使用该闭锁门电路就越困难。在 ADC 中，建立时间表示数据稳定时间比输入或输出 ADC 时钟边缘提前了多少。建立时间越长，捕获数据就越容易。这些规则在保持时间上也同样适用。

过程增益

与 SNR 的两个参数相比较，用户必须考虑到 ADC 的采样速率。信噪比可通过对收敛于奈奎斯特曲线的总体噪声底限进行积分得到。当然，用户的信号只会占据一些带宽；只有在这个带宽上的噪声才会影响到信号，而其他噪声可由数字滤波器滤除。对于相同的 SNR 而言，采样速率高的 ADC 噪声底限比较低。例如，一个 200kHz 带宽，信噪比为 90-dBFS 的 ∆∑ 型 ADC 的性能在理论上比产品说明书中规定的信噪比为 75-dBFS、100 MSPS 的 14 位 ADC—— ADS5424 要好。当然，如果在使用 ADS5424 对 200-kHz 带宽进行采样之后（明显超过 100 MSPS 的采样率），我们采用数字滤波来滤除带宽外的噪声（从 200 kHz 直到 50 MHz），ADS5424 的等效信噪比在这一带宽上为：

SNR200 kHz = 75 + 10×log10(50×106/200×103) = 99 dBFS >> 90 dBFS。

ADS5424 的信噪比将明显优于 ∆∑ 型 ADC（为了示例，假设噪声在奈奎斯特曲线上均匀分布，也就是说没有明显的闪烁噪声影响）。前述方程式的第二项称为过程增益。随着过采样比的增加，用户在相同信噪比每增加采样率一倍，噪声底限就会降低 3 dB。换言之，相关频带上的等效精度将增加 0.5 比特。

上一页  [1] [2] [3]  下一页