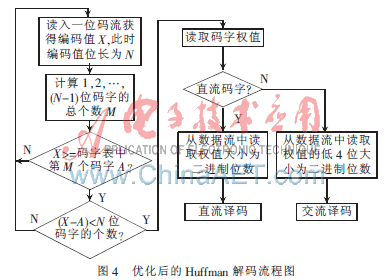
在JPEG文件中存储了两张量化表，分别为亮度量化表和色度量化表。反量化运算过程即为经HufFMan解码得到的系数矩阵与相应的量化矩阵相乘。由于数据是按8×8矩阵的“之”字行排列，所以要对反量化运算的结果进行反Zig-Zag操作。
　在解码8×8的数据块过程中发现，右下角的高频分量存在大量的０。如果完成Huffman解码之后，再进行反量化及反Zig-Zag排序，必然存在许多乘0运算及重复的数据存取操作，而且同时必须至少开辟两块8×8大小的SDRAM来存储这些数据，这样不仅浪费了时间也浪费了空间，不利于在小型嵌入式系统上的应用。因此，采取Huffman解码、反量化及反Zig-Zag三步合一的优化措施，Huffman解码出一个值后立即进行反量化、反Zig-Zag操作。但为了对应原来的存储顺序，需要建立这样一个对应存储位置的数组：

2.4 IDCT及浮点转整点运算
　在图形解码运算中，IDCT变换是主要运算，占用大量的CPU时间。若直接进行IDCT变换计算，一次二维IDCT变换需要1 024次乘法和896次加法，这样，在ARM7上解码800×600大小图像会相当慢，因此要提高解码效率，必须利用IDCT的快速算法。为此，本文采用了参考文献[6] ARAZ等人提出的IDCT快速算法。该算法的主要思想是：
　(1)将二维的IDCT分解为两个一维的IDCT降维处理，先后在行方向、列方向上做IDCT变换。
　(2)IDCT通过数学变换转化为离散傅里叶逆变换(IDFT)，然后利用矩阵变换简化计算。
　(3)减少乘法和加法运算次数。其结果是完成一次2D-IDFT仅需要10次乘法和29次加法。
原IDCT变换运算过程包含了5步计算，而本系统将其简化为3步，最大限度地减少数据存取操作次数。三角函数及一些固定的系数采用查表方式，除法运算的除数均为2的n次幂，可直接转换为右移操作，以减少计算量。但乘法和加法运算均为有符号浮点运算，而ARM7只支持整点运算，因此还需要将浮点运算转化为整点运算。
　在IDCT运算中，大部分的浮点乘法运算为一个数乘以一个余弦值(即乘数小于1)，根据这个特点，本文设计了如下浮点转整点运算方法：
　(1)将浮点数乘以256，得到的32位整点数格式为0xXXXXXX XX，高24位保留了浮点的整数部分及符号位，低8位保留到了小数部分的第4位。
　(2)乘法运算：被乘数转化为如上格式的32位整数(如0xAAAAAABB)，乘数要求小于1。转化后为8位整数，如0xCC。为了防止溢出，乘法运算做如下更改：
0xAAAAAABB×0xCC=(0xAAAAAA×0xCC)+((0xBB×0xCC)>>8)
　该方法能确保整个运算过程中数据不溢出。
2.5 色彩空间转换
　通过解码出来的Y(亮度)CrCb(色度)信号，要在屏幕上显示图像，还必须转化为RGB信号。其转换公式为：
　R=Y+1.402×Cb+128
　G=Y-0.344 14×Cr-0.714 14×Cb+128
　B=Y+1.772×Cr+128
　计算时，乘法运算使用上述的浮点转整点运算法则，但需要作如下修改：
　R=Y+Cb+Cb×0.402+128
　G=Y-Cr×0.344 14-Cb×0.714 14+128
　B=Y+Cr+Cr×0.772+128
　解码后的RGB信号直接存入显示缓存区，将实时显示在屏幕的对应像素点上，实现边解码边显示，直到整个图像全部显示在屏幕上。解码效果如图5所示，解码优化前耗时为30 s，优化后耗时为15 s，速度提高了一倍。

　本系统实现了JPEG图像通过LPC2478解码显示在像素为800×600的AA104SG02液晶显示器上，完成了基于LPC2478的图像解码及显示的硬件设计，成功将JPEG解码算法移植到本系统上，优化了解码算法。通过将优化后的Huffman解码与反量化、反Zig-Zag相结合，减少了乘零运算及数据存取操作、降低了内存消耗；引入快速IDCT算法，减少了乘法和加法运算次数；将浮点运算转换为整点运算，加快了运算速度、提高了运算精度。使复杂的JPEG图像解码在主频并不很高的小型嵌入式产品上得到了很好的实现。本系统可应用于控制系统的液晶桌面图片显示，为人机交互提供了友好的操作界面。
参考文献
[1] 张益贞，刘滔.VisualC++.实现MPEG/JPEG编解码技术[M].北京：人民邮电出版社，2002.
[2] 薛永林，刘珂，李凤亭.并行处理JPEG算法的优化[J].电子学报，2002(2).
[3] 董岚，李丽，张宇昂.基于AMBA2AHB总线多核平台的JPEG解码[J].电子测量与仪器学报，2009，23(2).
[4] NXP SEMIconductors. LPC24XX user manual. Rev. 04-26，August， 2009.
[5] Mitsubishi EleCTRIC Corp. Telchnical specification Aa104sg01. Mar.9， 2006.
[6] ARAI Y， AGUI T， NAKAJIMA M. A fast DCT-SQ scheme for images[J]. IECE Transactions 1990，71(11)： 1095-1097.

上一页  [1] [2]