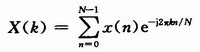3 基于滑动DFT的AM信号数字化解调算法
    以上两种方法都是对调制信号本身进行处理的，在频域角度，常用FFT算法对信号进行解调，但这种方法计算量较大，且耗时，这里介绍采用滑动DFT算法对AM信号进行数字化解调。该方法相比于传统的FFT算法计算量大大降低，具有较高效率。
    经A／D采样后的离散信号表示为：
    x(n)=Acos(ωc／fsn+φ)， -∞≤n≤+∞
    式中：fs为A／D采样频率；A，ωc和φ分别对应信号幅度、载波角频率和初相。
    窗口截取信号表示为：

    故在解调过程中，仅对载波频率处所对应的DFT幅度感兴趣，取其幅度值去掉直流分量即可恢复原始调制信号。具体运算推导过程如下：
    对窗口内的信号在K0=Nfc／fs频点作DFT变换：
   
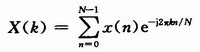
    设滑动窗口长度为L，DFT运算点数为N，用X1(K0)表示从第一个采样数据开始的L个采样数据进行DFT运算，得到的在频点K0处的傅里叶值，则有：

    这样即可得到全部采样数据点在频点K0处对应的傅里叶值。随后只需计算|Xn(K0)|，去除直流分量即可恢复调制信号。
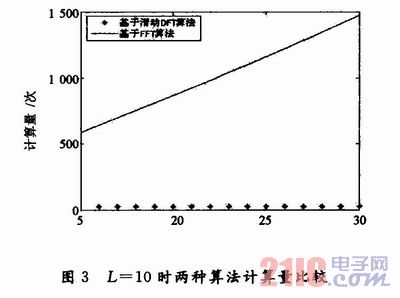
    传统的FFT算法对窗口内的所有时刻都要独立运算L次，而每个时刻都要Nlog：N次复乘运算口]，总计算量为LNlog2N。利用滑动DFT算法，在已知前个时刻频谱Xn-1(K0)的情况下，计算Xn(K0)只需2次复乘运算，对窗口内的所有时刻总计算量为log2N+2(L-1)。通过图3的比较可以明显看出，当N较大时，滑动DFT的计算量远小于FFT。

上一页  [1] [2] [3]  下一页