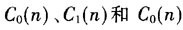·上一文章：中冷器堵塞导致柴油机断裂不足
·下一文章：借助Usboot软件修复TF卡
中，找到3组相关序列的最大值，根据最大值对应的位置和相关序列确定PSS的定时同步A和
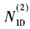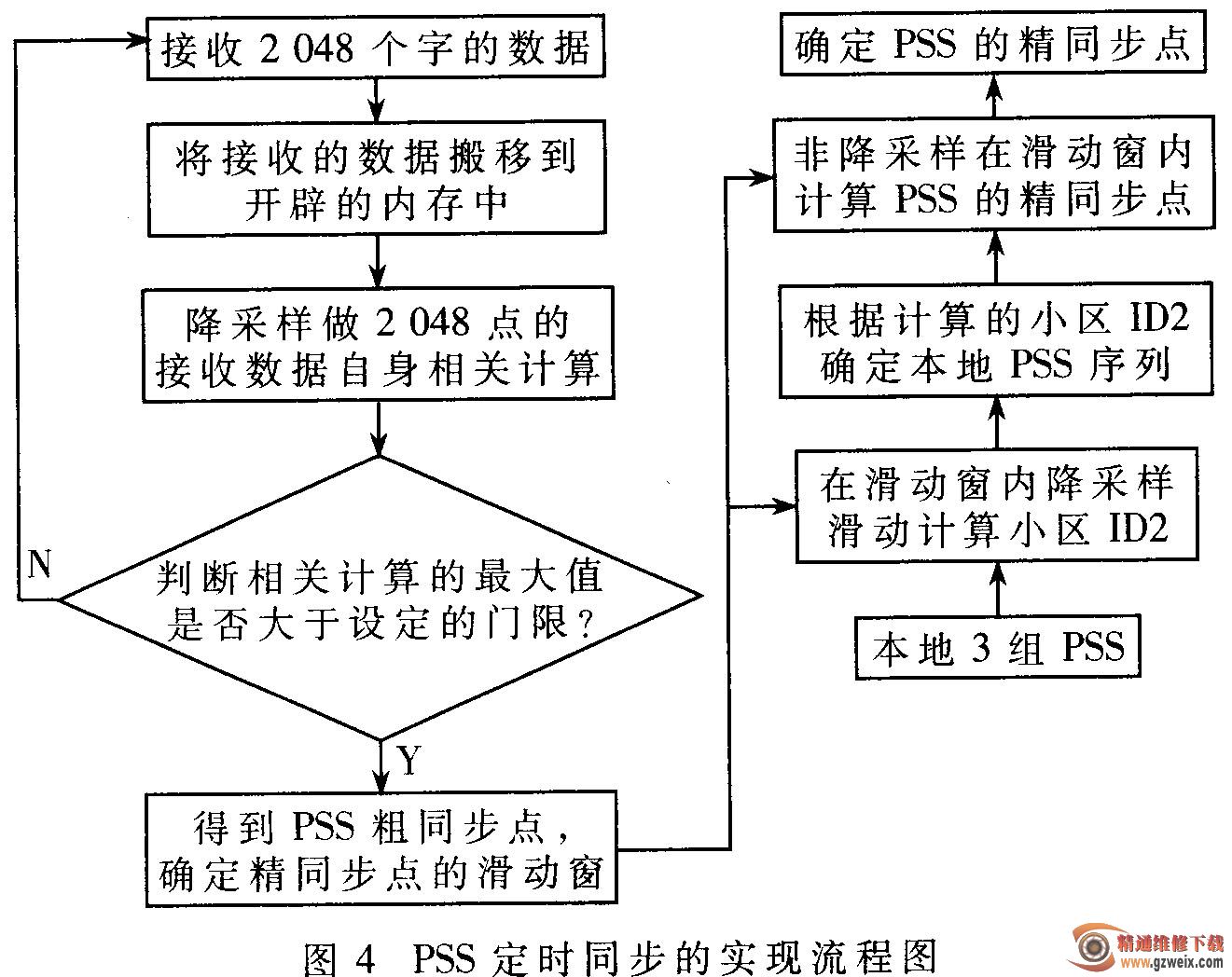
的值。该方案虽然能够计算出PSS定时同步点的位置和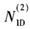
，但即使采用降采样也存在计算量太大、复杂度太高的问题，并且在接收数据时需要开辟的内存空间较大，最大开辟的空间为153 600个字。为了减少计算的复杂度和内存空间问题，需要对PSS定时同步进行改进，具体可以分为以下5个步骤：
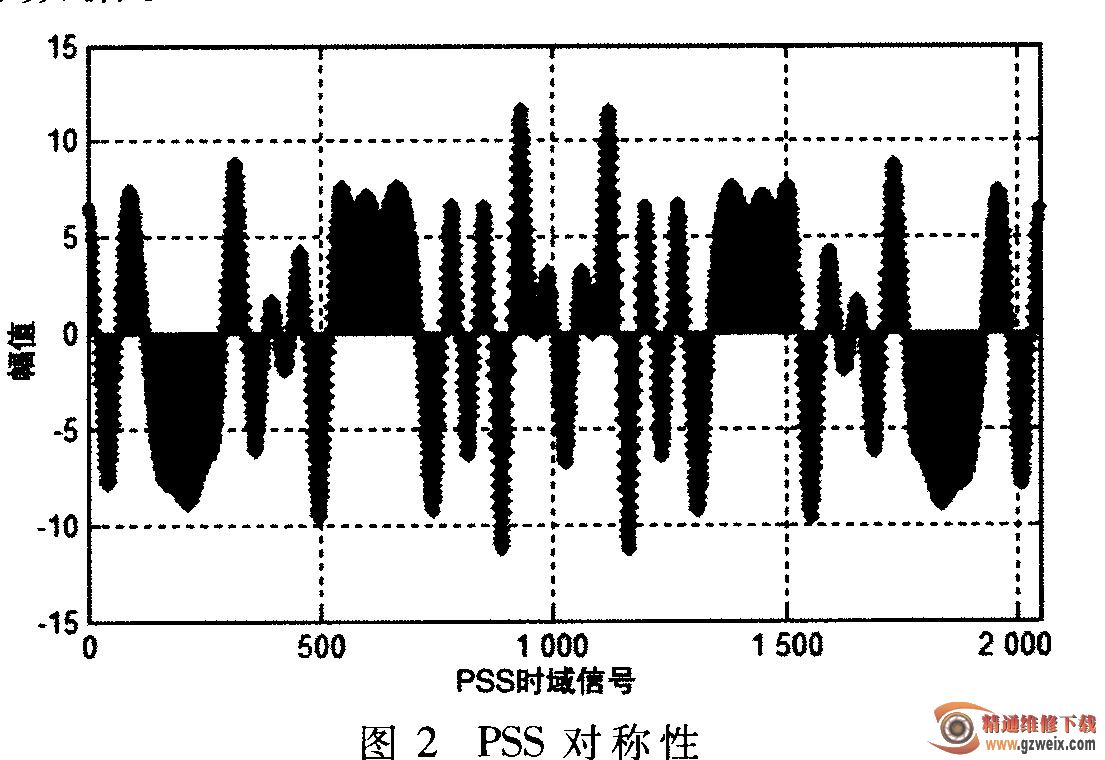
(1)频域的PSS序列是Zadoff-Chu序列，由Zadoff-Chu序列的性质可知，该序列关于中心点对称。将频域PSS序列经过IFFT变换到时域后，该序列仍具有良好的对称性。如图2所示，在实际处理中，可以将PSS做成表格存储起来，通过直接查表的方式减少计算时域PSS的处理时间。根据PSS的对称性，每组PSS只需要存储1 024个字的数据。
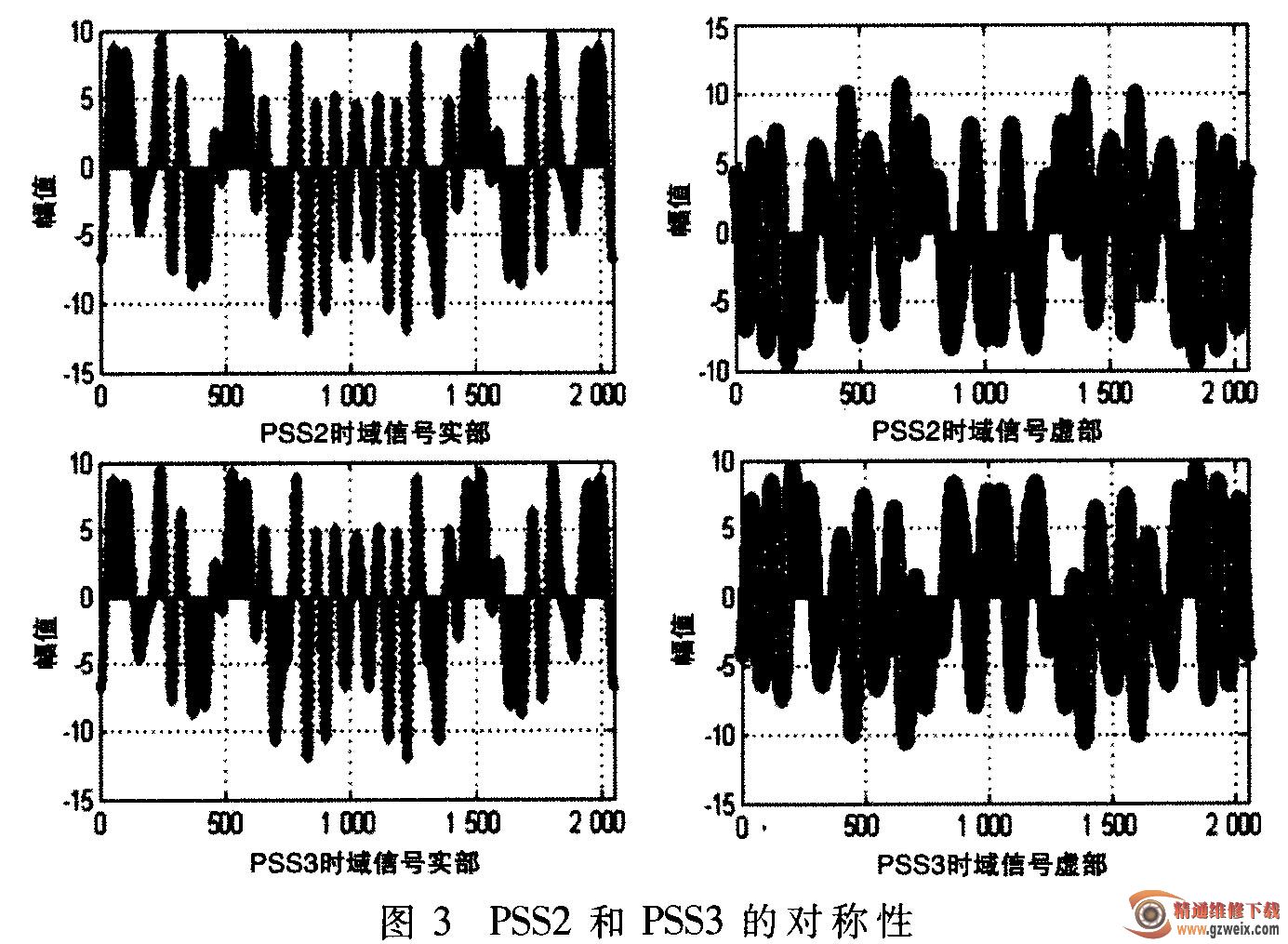
(2)根据Zadoff-Chu序列的性质有：当根序列号之和等于序列的长度时，这两个序列的实部相等、虚部相反。结合Zadoff-Chu序列的对称性，可以得出根序列号u=29的时域PSS和u=34的时域PSS的实部数据相同、虚部相反，如图3所示。因此实际处理中，只需要存储2组u为25和29时的时域PSS数据即可，且每组的数据只需存储1 024个字。这样整个本地的PSS存储占用的内存空间为2048个字。
(3)根据步骤(1)和(2)中分析的PSS的性质，在计算PSS定时同步的位置时，可以采用PSS自身良好的中心对称结果进行相关计算，将接收数据PSS的同步点的位置确定后，再将接收的PSS和本地3组PSS进行相关计算，最终确定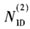
的值。这样可以大大简化计算的复杂
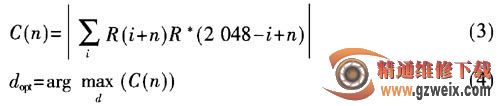
由式(3)可计算出PSS的定时同步点的位置Dopt。确定PSS同步点位置Dopt后，和本地3组PSS进行相关计算确定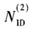
的值，计算公式如下：
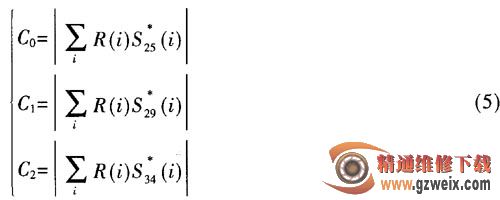
式中，如果最大值为C0，则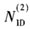
为0；如果最大值为C1
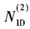为1；否则
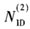为2。
(4)为了进一步减小计算的复杂度，可以将接收端数据进行降采样后再进行自身的相关计算。降采样后相关计算得到的PSS的定时同步点与理论上存在偏差，偏差的大小与降采样的点数有关。因此在确定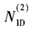
时，在已计算的粗同步点的基础上选取左右偏差一定的范围降采样后进行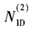的计算；确定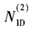后，再次采用非降采样滑动相关计算确定同步点的位置。
(5)为了减小开辟内存空间问题，采用接收数据进行实时处理，即一边接收数据一边进行相关计算，这就要求在下一次接收数据到来之前需要完成前一次接收数据的处理。
2实现及仿真
由上述理论分析，可以得到如图4所示的PSS定时同步的实现流程图。
