信号处理中，频率是信号最重要的表示。传统的傅里叶变换分析方法并不能分析出信号的某一频率在甚么时刻出现，为此产生了能同时在时间和频率上表示信号密度和强度的时频分析，如短时傅里叶变换和小波变换等，但其基本思想都是根据傅里叶分析理论，对非线性非平稳信号的分析能力不足，受限于Heisenberg不确定原理。HHT ( Hilbert Huang Transform)是由N. E.Huang 等人在1998 年提出的一种崭新的时频分析方法，能够对非线性非平稳的信号进行分析，同时具有良好自适应性的特点。其本质是对信号进行平稳化处理，将具有不同时间尺度的信号逐级分解开来。

　　HHT 方法在各领域已得到了广泛应用，但依然存在一些不足，例如易产生虚假分量和模态混叠等。针对传统经验模式( Empirical Mode Decomposit iON，EMD)分解方法所导致的模态混叠现象，法国以Flandrin 为首的EMD 算法研究小组和Huang 本人的研究小组通过对EMD 分解白噪声结果统计特性的大量研究，提出通过加噪声辅助分析( NA DA ) 的EEMD ( EnsembleEmpirical Mode Decomposition) 方法，将白噪声加入信号来补充一些缺失的尺度，在信号分解中具有良好的表现。

　　EEMD仿真系统的实现利用了Matlab 平台，通过GUI 控件实现了系统设计，能直观方便地进行比较分析，验证了EEMD 在抗混叠方面较原有方法的改进。

　　1   经验模式分解( EMD) 和IMF

　　HHT 方法包含两个主要步骤:

　　( 1) 对原始数据进行经验模式分解( EMD) ，把数据分解为满足Hilbert 变换要求的n 阶本征模式函数( IMF) 和残余函数之和。

　　( 2) 对每一阶IMF 进行Hilbert 变换，得到瞬时频率，从而求得时频图。

　　函数必须关于时间轴局部对称，且其过零点与极值点个数相同。此类函数被称为固有模态函数( Int rinsicMode Function，IMF) 。

　　经验模式分解方法能把非平稳、非线性信号分解成一组稳态和线性的序列集，即本征模式函数。根据Huang 的定义，每一阶的IMF 应满足两个条件:

　　( 1) 数据的极值点和过零点交替出现，且数目相等或最多相差一个任何点上；

　　( 2) 在任何点上，有局部最大值和局部最小值定义的包络的均值必须是零。

　　其筛选算法如下:

　　( 1) 对于输入信号x ( t) ，确定x ( t) 所有极值点。

　　( 2) 用三次样条函数对极大点和极小点分别进行拟合得到x ( t) 的上下包络线。

　　( 3) 用原始数据序列减去上下包络线的均值。

　　平均曲线：

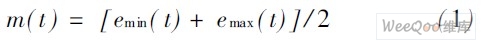
　　细节信号：

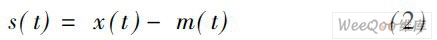
　　( 4) 通常s( t ) 还不满足IMF 的条件，需重复进行以上步骤，进行迭代处理，H uang 给出的迭代停止准则为：

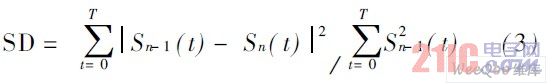
　　SD 是筛选门限值，一般取值为0. 2~ 0. 3，若计算SD 小于这个门限值，筛选迭代将会结束。

　　经过n 次迭代满足停止准则后得到的sn ( t) 即为有效IMF，剩余信号则进入下一轮筛选过程。

　　经过多次筛选后，原始数据序列被分解为一组IMF 分量和一个残余量，得到的IMF 都是平稳的，通过Hilbert 变换得到的结果能够很好地分析非线性非平稳的信号。

　　2   传统EMD 的不足与缺陷

　　当信号的时间尺度存在跳跃性变化时，对信号进行EMD 分解，会出现一个IMF 分量包含不同时间尺度特征成分的情况，称之为模态混叠。

　　模态混叠的出现一方面和EMD 的算法有关，另一方面也受原始信号频率特征的影响。

　　Huang 曾经提出了中断检测的方法来解决模态混叠现象，即直接对结果进行观察，如果出现混叠则重新分解，这种方法需要人为后验判断。

　　重庆大学的谭善文提出了多分辨率的EMD 思想，对每一个IMF 规定一个尺度范围来解决模态混叠，但是这种方法牺牲了EMD 良好的自适应性。