·上一文章：研究基于IEEE1149.7标准的CJTAG测试设计方法
·下一文章：基于移动预测的垂直切换算法
Vogt后来又提出一种不同的估计方法，根据切比雪夫不等式：一个涉及随机变量的随机试验过程其输出很可能在该变量的期望值附近。因此，可以用读取结果与期望值之间的取得最短距离时的数值来估计标签数目。估计模型如式(3)所示：
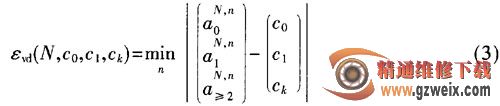
其中，c0、c1、ck为实际测得的成功、空闲、碰撞时隙数值。
在标签数量N取值范围［C0+2Ck, …,2(C1+2Ck)］内找到最小的二值，所对应的N就是估计的标签数量。
除此之外，还有基于Bayesian理论的后验概率估计方法，其系统效率有所提高但计算复杂度也变得很高。ISO-18000-6C标准中使用的Q算法对系统的吞吐率作了一定的改进。但是，既然是估计算法就必然会存在估计误差，估计算法的效果影响着系统效率。为改善估计误差对系统效率的影响，本文提出了改进方法。
2 FBC_DFSA算法及其仿真
时隙帧识别法都涉及到标签估计，但这些估计算法显然都存在误差。因此，本文提出FBC_DFSA算法，用估计算法得到的标签数来设置帧长，在进行一轮识别后得到的测量结果反馈到前面估计得到的标签数目，与其进行对比，检验估计算法的准确性并做出调整。本算法的原理模型如图2所示。
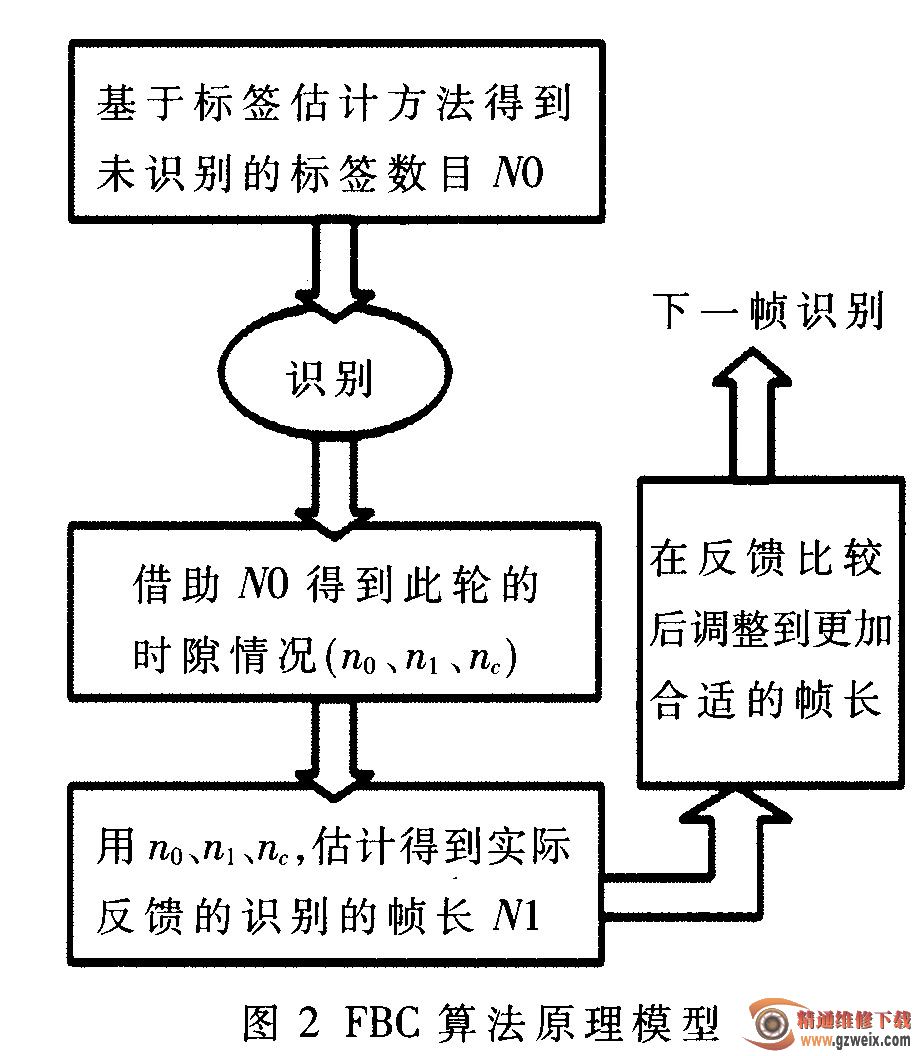
首先看一下基于空闲时隙、成功时隙、碰撞时隙的一系列标签估计，假设n个标签在某个帧选择了其中第i个时隙的标签数目，概率分布为：
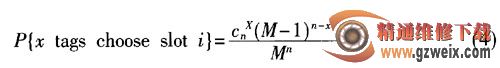
M为一帧内时隙数。如果该时隙为碰撞时隙，x≥ 2。得到x标签选择识别时隙的概率分布为：
Px{x个标签Ii是碰撞实习}=
可得到选择时隙i标签数目的平均值：
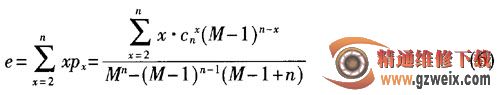
其实可以看到，当e=2和e=2.39时，分别为lower-bound和Schoute估计结果。Vogt方法是通过比较一个向量组中与期望值的距离来得到最佳标签数，Bayesian算法用后验概率分布来估计识别的标签数目。但是，基于向量空间的搜索法（Vogt）和基于后验概率分布法(Bayesian)尽管在系统效率上有些改进，但是计算复杂度也比较大[9]。如图3算法模型，基于lowerbound和Schoute的标签估计 DFSA方法来验证FBC_DFSA算法。
