·上一文章：排除大众帕萨特防盗系统故障
·下一文章：研究一种新型的超宽带天线
从上面得到的最终时频图上可以得到信号每一跳的频率、驻留时间和跳时[8]。经过STFT及形态学处理后的时频图，其横轴是时间轴，纵轴是频率轴。对跳频信号而言，其所占的长度在横轴上的投影即为该跳信号的驻留时间Tdw；每一段短线段所占的高度在纵轴上的投影即为该跳信号的瞬时频率Fs。求取跳频信号频率集及跳周期的步骤为：
(1)延频率轴寻找每跳信号起始、结束索引Fstart、Fstop。求取该跳纵轴索引对应的频率值即瞬时频率为：
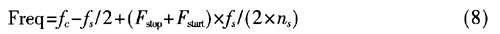
其中关为信号的中心频率不为采样率，ns为每个STFT时间窗内进行STFT信号的个数；
(2)沿横轴寻找每跳信号起始、结束索引Tstart, Tstop。求取该跳的起始和结束时间，即横轴索引对应的时间值为：
其中N为信号总点数，nt为STFT时间窗数,Fs为信号采样率。该跳的跳时刻即为Startt。
(3)跳周期TD等于跳时刻差分后的均值，即：
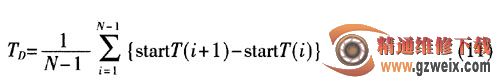
由于短时傅里叶变换导致的频率分辨率的局限性，短时傅里叶变换点数选择较小时可能会导致频率很接近跳频信号在时频图的纵轴上产生重叠。若频率轴上出现重叠的情况，则判断这两跳信号的时间间隔，若时间间隔在一定范围内，则认为它们是同一跳信号，否则认为它们是不同跳信号。
2实验及结果分析
由信号源发出一跳频信号，包含4个不同频率，采样率为125 kHz，中心频率为88.05 kHz，跳频频率为188.514, 88.029, 88.039, 88.0321，跳周期为80 ms。取频率分辨率为25 kHz，对其进行短时傅里叶变换，并经二值化处理，得到跳频信号原始时频图，如图1所示。
为了从复杂的信道环境中提取出跳频信号，应对时频图进行进一步的形态学滤波处理。首先进行图像开处理，以滤除雾态噪声。通过实验验证，开运算的结构元素选择宽625个点，高1个频率分辨率的矩形效果较好，经过开处理后的时频图如图2所示。其次进行图像闭处理，提取定频信号。闭运算的结构元素选择宽375个点，高1个频率分辨率的矩形窗。经过闭运算后提取出来的定频信号。这样的结构元素能够抑制谱图中的波谷噪声，填平杂散负脉冲；也符合跳频信号形态特征，在一定程度上恢复了由去干扰处理导致的信号形态缺失。
再将除去杂散噪声后的时频图与提取出的定频信号进行式（7）的运算，便可以提取出跳频信号，如图3所示。可以看出，通过形态学处理，噪声剔除效果较好，且基本未对原有的跳频信号产生影响。在求取跳周期时，由图3跳频信号时频图可以看出，信号存在第一跳和最后一跳两个不完整的跳频周期，它们会对跳频周期的估计产生较大的影响，而这两跳之间的跳频信号都是完整的，对跳频周期的估计没有影响。所以在估计跳频周期的过程中，用第一跳与最后一跳之间的跳时刻的差分均值求取跳周期。
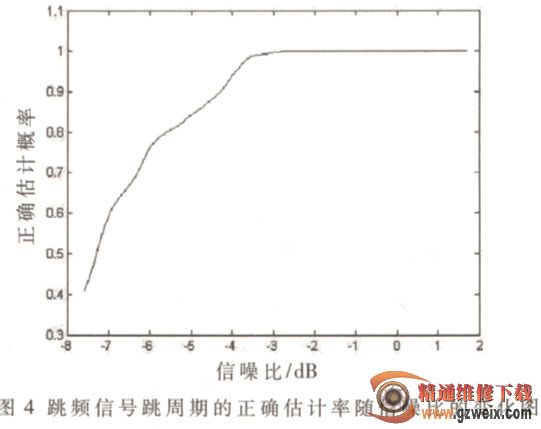
为验证本文方法在不同信噪比的情况下对跳频参数估计性能的影响，对[-8 dB, 2 dB]之间的不同信噪比下的信号分别进行100次实验，得到跳频信号跳周期的正确估计率随信噪比的变化图，如图4所示。从图4中可以看出，当信噪比高于-3 dB之后，对跳频信号跳周期的正确估计率达到95％以上。跳频信号跳频频率的正确估计率随信噪比的变化如图5所示。由图5可知，当信噪比高于-5 dB之后，对跳频信号跳频频率的正确估计率达到98％以上。
