--- 4.3 均衡

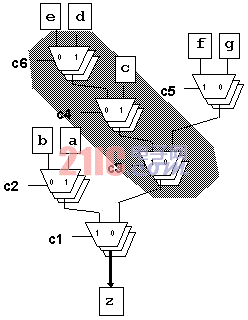
--- 压缩通过转换2:1复用器三联，能够减少实现复用器总线所需的4-LUT数量。但是，如果不进行复用器树重构，有些结构是不可能得到最佳三联分组的。例如，无法将图10中所有的2:1复用器进行分组，这是因为每一种可能的分组都将会剩余一个2:1复用器而无法处理。

--- 均衡的目的在于通过最少的重构得到最佳的压缩。对于图10的例子，可以采用图11所示的方法，得到两组2:1复用器三联。

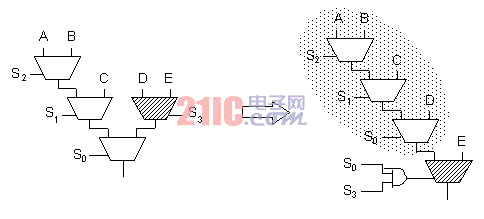
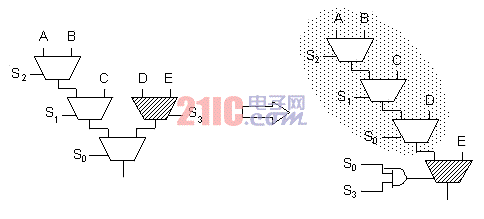
--- 均衡算法由图12的递归定义。由首复用器开始，算法首先均衡复用器树左面和右面数据输入。均衡返回还没有连接为三联的2:1复用器的数量。均衡确保形成尽可能多的三联，这样只会剩余一个或者两个2:1复用器，甚至没有剩余。

--- 均衡中的任何阶段，都需要对1～5个2:1复用器进行均衡（从左侧分支开始最多两个，从右侧分支开始为两个，还要算上当前的2:1复用器本身）。1或2个复用器不会形成更多的三联，而3个复用器总是能够形成三联。4或5个复用器则需要进行重构，以免剩余无法处理的复用器，这种重构方法在图13和图14中示出。

图10 复用器树次优压缩的例子

图11 由均衡未完善压缩


图12 均衡算法

图 13重构4个复用器实现均衡


图14 重构5个复用器实现均衡

5. 算法总结

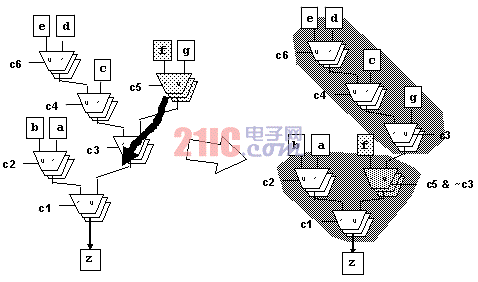
--- 本文引入了复用器树总线概念，描述了可用来提高压缩性能的均衡方法，压缩以效率更高的4:1复用器来替代2:1复用器三联。图15显示了全部复用器重构算法。

--- 复用器重构算法性能依赖于对较大复用器树总线的识别。由于复用器重构算法在整个总线上分担控制逻辑，因此，总线越宽，压缩的效果就越明显。优化会减小复用器树间的相似性，从而减小所寻找的总线宽度，因此在复用器重构之前，应尽量避免优化。

--- 复用器重构以分解大的复用器为2:1复用器开始。设计中所有2:1复用器都用于形成4.1节所描述的复用器树。结构相似的复用器树然后合并形成4.1节中的总线结构。

--- 算法的主要部分依次优化每一个总线。均衡将2:1复用器重新排列为三联，这样在压缩阶段，每个三联能够重新编码为效率更高的4:1复用器。

6. 结果

--- 本文所阐述的算法已经集成到Altera Quartus II 4.2综合软件中。图16显示120个真实用户设计中，Altera基准测试的面积减小结果。

--- 结果表明，一小部分设计所需的LUT数量减小了20%，超过四成的设计面积减小了5%以上。所有设计面积平均减小了4.2%。

--- 据估算，面积减少平均4.2%意味着复用器平均减少了17%。

--- 复用器重构主要集中在减小面积上（例如，减少所需4-LUT的数量），而且对电路速率影响不大，电路平均速率仅降低1%。

7. 结论

--- 本文阐述了复用器重构算法，该算法能够将设计中实现复用器所需的4-LUT数量平均减少17%。

--- 复用器重构算法的关键在于优化复用器总线。即使附加了控制逻辑，新优化算法仍能够减小总线上每个比特位的面积。这是由于控制逻辑可以由总线共享，其面积代价可以抵消。

--- 压缩将2:1复用器三联转换为有效的4:1复用器。尽管可能需要附加LUT对4:1复用器控制线进行重新编码，这种代价可以通过采用复用器总线整体压缩方法来抵消。此外，通过构建最大的复用器树，可对大量的2:1复用器三联进行转换。

--- 本文还引入了能够提高压缩算法效率的均衡方法。本文描述了面向基于4-LUT的FPGA算法，例如Altera Stratix I和Cyclone器件。新的FPGA体系结构可使用不同大小的查找表（如Stratix II体系结构能够采用4、5、6输入LUT）。可采用本文阐述的方法来进一步减小这些体系结构的面积。

上一页  [1] [2] [3]  下一页