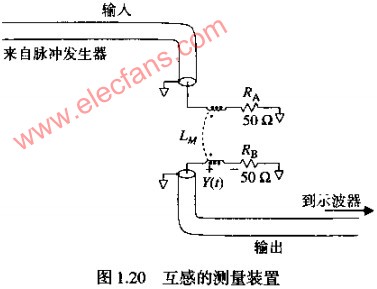
图1.20描述了互感的一种简单测量方法。

与“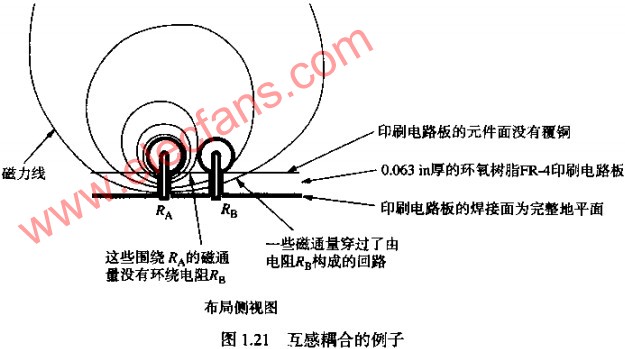

包围电阻RB的磁力线被认为是穿过了电阻RB形成的回路。当我们提及电阻RB形成的回路时，设想一个起始于RB接地端的电流环。电流从这里通过RB进入同轴电缆探头，通过同轴电缆到示波器的内部端接电阻RT，经过这个电阻到示波机壳，由电缆的屏蔽层返回到本地的地平面，再从地平面回味到RB。穿过这一回路的总磁通理的任何变化都会在该回路上产生一个电压。

由于RB和RT的电阻值相等，感应电压在它们之上的分压相等，因此显示在示波器上预期电压只有总感应电压的一半。如果同样物理尺寸的电阻RB是一个0欧的电阻，则会在示波器上看到全部的感应电压。

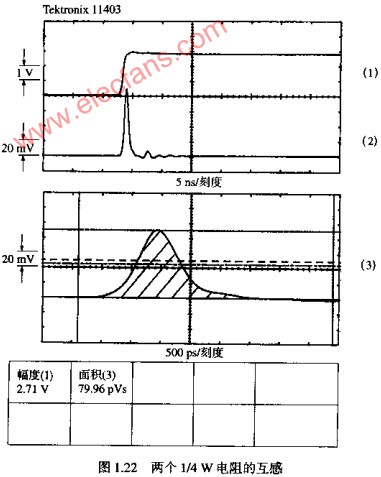
从图1.22的测量结果可以估算出感应系数，则于接收到的信号被二等分，记住要乘以2：

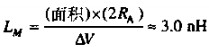
其中，面积=80PVS

      △V=2.7V

      RA=50欧

更精确定电感的方法应该是，从测量面积中减去已确定的互容耦合部分，然后采用修正后的面积计算电感，则“互容的测量”得知，互容干扰的面积是56/6PVS，由于每个电阻接地，采用一个因数6修正图1.17中的测量结果。

修正后的面积为：面积=80-56/6=71PVS

然后，修正后的互感是：LM=（面积）*（2RA）/△V=2.6NH

现在，从推出的面积过来看是否能预测图1.22中的峰值干扰。采用式：L=[面积/△L]中的峰值干扰。采用式：面积=80-56/6=71PVS，由于感应信号在RB和RT之间的分压，注意应该除以2。

LM=2.6NH

TR=800PS

RA=50欧

串扰电感=LM/2RAT=0.032

加上例1.3的容性串扰：串扰电容=0.025/6=0.004

                     串扰总=串扰电感+串扰电容=0.036

比较上式，基于测量面积的预测值与图1.22中实际测量的峰值干扰：

串扰=（4.6刻度）*（20MV/刻度）/（2.7刻度）*（1V/刻度）=0.034