式中，θ是导模在环中每圈的相位增加，α代表导模在环中的损耗，包括传播损耗和环的弯曲损耗，t=∣t∣exp(jϕ)是复系数，表征的是没有被耦合进环形波导内的长直中的那部分导模。

3模拟仿真分析

仿真分析时，光源可采用平面波TM模，边界条件选取APML。图2所示是对该模型进行的仿真图。由图2可见，光在通过长直波导时，一部分光耦合进了环状波导。



图3所示是R=1μm时，端口2(蓝色)和端口1(红色)出射归一化强度曲线，从图3可以看出，透射强确实随波长有周期性变化，在所示波长范围内出现了两个吸收峰(absorption peak)，从透射公式(2)中可以得出，环的半径是影响透射结果的重要因素，为利于对比，接下来将半径改为1.1μm，并进行仿真，从而得到了图4所示的出射归一化强度曲线。



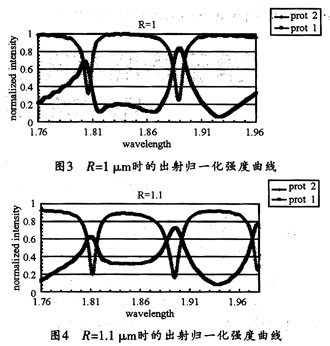
对比图3和图4可以看出，当R从1 μm变化到1.1 μm，吸收峰的位置整体向右偏移了，并且出现了3个吸收峰，R=1.1μm消光比(extinction ratio)要比R=1 μm时更大，吸收峰同样尖锐。图3中较好的1.8μm到1.9μm处的两个吸收峰的消光比大约是8db，-3db带宽大约是8nm，好于现有水准。另一个重要的衡量滤波器的系数是FSR(passband bandwidth and extinction ratio)，在本文中，可以简单地理解为相邻吸收峰的距离，R=1μm时是90 nm，同样波长范围内，R=1.1时则出现了3个吸收峰，说明当R变大时，FSR反而变小，经测量大约是86 nm。可以推断，当环继续增大，吸收峰间距也许能满足DWDM的需要，从而为DWDM大型集成化提供可能。

4 结束语

本文分析了基于表面等离子激元的可调谐共振环滤波器结构原理，并分别对环半径R为1.0μm和1.1 μm时进行了仿真。结果发现，波导环半径的变化会周期性地在特定波长上产生强烈的吸收效果，其中-3 db带宽只有8 nm，好于现有水准，且随着环半径R的增大，吸收峰会向右移动，而且可以通过改变金属温度的方法对滤波器进行调谐。通过计算在所示波长范围内，所有峰的数量可知，随着环状波导半径R的增大，吸收峰会更密集(FSR减小)，而当环的半径继续增大，吸收峰间距越来越小，但峰依然尖锐，可以符合密集波分复用(DWDM)的需求，应用前景光明。另外，本研究模型结构简单，整个模型大小不超过10μm2，而且比现有的光子晶体器件小，很易于集成。

上一页  [1] [2]