引言

　　现代雷达普遍采用相参信号来进行处理，而如何获得高精度基带数字正交(I，Q)信号是整个系统信号处理成败的关键。传统的做法是采用模拟相位检波器来得到I、Q信号，其正交性能一般为：幅度平衡在2％左右，相位正交误差在2°左右，即幅相误差引入的镜像功率在-34 dB左右。这样的技术性能限制了信号处理器性能的提高。为此，近年来提出了对低中频直接采样恢复I、Q信号的数字相位检波器。随着高位、高速A／D的普遍应用，数字相位检波方法的实现已成为可能。本文介绍了一种正交相干检波方法，并给出了其FPGA的实现方案。

　　1 基本原理

　　1．1 中频信号分解的基本原理

　　一个带通信号通常可表示为：

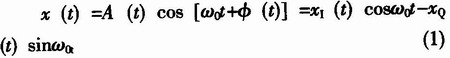
　　其中，xI(t)、xQ(t)分别是s(t)的同相分量和正交分量。ω0为载频，a (t)、φ(t)分别为包络和相位。它们之间具有如下关系：

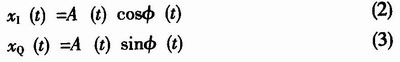
　　所构成的复包络信号为，该信号包含了式(1)中的所有信息。

　　要对中频信号进行直接采样，首先要保证采样后的频谱不发生混叠。根据基本的采样理论，即Nvquist采样定理要求以不低于信号最高频率两倍的采样速率对信号直接采样，才能保证所得到的离散采样值能够准确地确定信号。然而，如果信号的频率分布在某一有限频带上，而且信号的最高频率fH远大于信号的带宽，那么，此时若仍按Nyquist采样率来采样，则其采样频率就会很高，以致难以实现，或是后续处理的速度不能满足要求。因此，此时就要用到带通采样理论。

　　所谓带通采样定理，即设一个频率带限信号选x(t)，其频带限制在(fL，fH)内，此时，如果其采样速率满足：

　　式中，n取能满足fs≥2(fH-fL)的最大正整数(O，1，2，……)，则用fs进行等间隔采样所得到的信号采样值就能准确地确定原始信号。

　　式(4)中的fs用带通中心频率f0和频带宽度B可表示为：

　　其中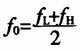，，n为整数，且要求满足fs≥2B，B为信号带宽。

　　值得指出的是，上述带通采样定理适用的前提条件是：只允许在其中的一个频带上存在信号，而不允许在不同的频带上同时存在信号，否则将会引起信号混叠。

　　1．2 Bessel插值法基本原理

　　设A／D变换输入的窄带中频信号为：

　　式中，A(t)为幅度，f0为中频频率，φ(t)为初相，τ为回波脉冲宽度。

　　假设式(5)中n=2，则采样频率。事实上，若对窄带中频信号采样，则第N个采样点离散形式为：

　　式中，为采样间隔。

　　另外，由贝塞尔内插公式知，其8点中值公式为：

　　式中，I2、I4、I6、I8为已知点，为，I2、I4、I6、I8的中值点。

　　在实际应用中，考虑到FPGA的特性，可将

　　(8)式改写成以下形式：

　　这样，对于下列时间序列：Q1、I2、Q3、I4、Q5、I6、Q7、I8，按式(9)即可求出，而Q5即为两组正交信号。由此就可得到内插运算的原理框图如图1所示。

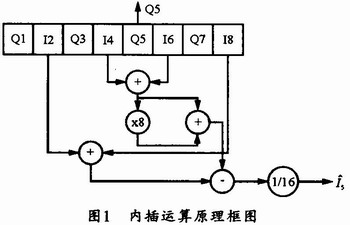
　　2 基于FPGA的实现方案

　　首先将输入FPGA的一路12位数字信号中的每一位都与时钟信号进行异或运算，以使I’(n)=x(2n)(-1)n和Q’(n)=x(2n+1)(-1)n+1，从而达到符号修正的目的。经过修正，输出的数字信号序列是一个由I的偶数项和Q的奇数项交替出现所组成的序列，即：I0，Q1，I2，Q3，I4，Q5，…，I2n，Q2n+1…。为实现Bessel插值，还需要得到某时刻Q2n+1值所对应的I的偶数项(I2n-2，I2n，I2n+2和I2n+4)。鉴于移位寄存器有延时功能，可使用12片移位寄存器74164取出I的偶数项序列，同时分离的还有相应的Q2n+1一路信号。接着，I的偶数项序列经过加法器电路进行有符号加、减法运算。由于Bessel插值中的分母均为2的整数幂，因而用右移来实现2的整数幂除法非常方便。其实现框图如图2所示。

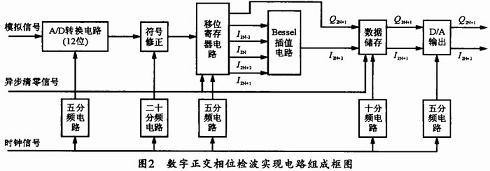
　　该FPGA实现方法，由于只涉及移位、简单门和加减法运算，因此，用FPGA实现起来很方便，也可以获得较高的运算速率。

　　3 基于FPGA的硬件仿真结果

　　为便于观察，仿真时可设定输入信号A (t)为常数，A／D的采样率fs为8 MHz来对信号进行中频采样并插值，以得到二路正交信号。运用QuartusⅡ的仿真结果如图3所示。

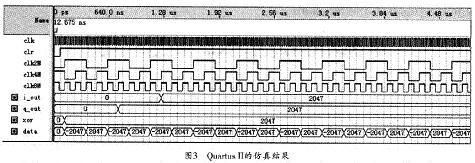
　　图3中，data为A／D采样后的输入信号，xor为符号修正后的信号，i_out，q_out为输出信号。

　　之后，将仿真程序 下载 到电路板中的FPGA(使用的是ALTERA公司的EPlC3T144C7芯片)中，便可用示波器观察到如图4所示的仿真结果。

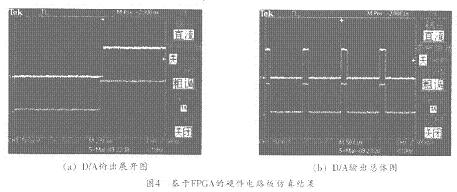
　　从图4可以看出，I，Q两路输出为相似的波形，符合前面的设定A(t)为常数；其中图4(a)为图4(b)的展开图，由图4可以看出，I，Q两路信号存在相位上的差异。

　　4 结束语

　　本文详细介绍了中频直接正交采样及Bessel插值理论，并基于这一理论，用FPGA将一路中频信号分解成了两路正交数字信号，本文同时重点给出了用FPGA实现这一过程的详细方案。