摘要：在数字信号处理应用中，滤波占有十分重要的地位，如对信号的过滤、检测、预测等，都要广泛地用到滤波器。文中研究了FIR滤波器窗函数算法的基本思想给出了在定点DSP芯片上实现FIR数字滤波器的设计方法，并给出了仿真结果。
关键词：DSP；FIR滤波器；循环寻址；汉宁窗

0 引言
    数字信号处理现已在通信与信息系统、信号与信息系统、自动控制、需达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。在数字信号处理应用中，滤波占有十分重要的地位，如对信号的过滤、检测、预测等，都要广泛地用到滤波器。IIR数字滤波器的设计保留了一些典型模拟滤波器优良的幅度特性，但所涉及的滤波器相位特性一般是非线性的，而FIR滤波器则可在保证幅度特性并满足技术要求的同时，也很容易做到严格的线性相位特性。

1 基于窗函数法的FIR滤波器设计
1．1 单位冲激响应
    首先应根据技术要求确定待求滤波器的单位冲激响应hd(n)。如果给出待求滤波器的频率为，那么单位取样响应则可用下式求出：
   
    当较复杂或不能用封闭公式表示时，就不能用上式求出hd(n)。此时可以对从ω=0到ω=2π采样M个点， 采样值为，k=0，1，2，…，M-1，并用2π/M代替(1)式中的dω，此时(1)式可近似写成：
   
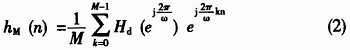
    这样，根据频率采样定理，hM(n)与hd(n)应满足如下关系：
   
    因此，如果M选得较大，就可以保证在窗口内，hM(n)有效逼近hd(n)。实际计算(2)式时，可以用的M点采样值，来进行M点IDFT
(IFFT)，从而得到(2)式的值。
    如果给出通带阻带衰减和边界频率的要求，则可选用理想滤波器作为逼近函数，从而用理想滤波器的特性作傅立叶逆变换，以求出hd(n)。若理想低通滤波器为：
   
    那么，求出的单位取样响应hd(n)则为：
   
    为保证线性相位，通常应取α=(N-1)／2。