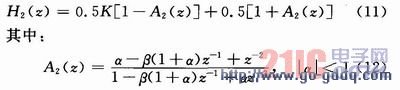摘要：对一阶、二阶可变参数数字均衡器的设计进行了研究，给出了数字均衡器的数学模型，得出了数字均衡器的频响特性曲线，分析了参数变化对数字均衡器频响的影响，并进行了实例分析。结果表明，对音乐信号处理，按照频响要求设定好均衡器的可变参数，就可很方便地设计出满足要求的数字均衡器，达到改善音质的目的。
关键词：音乐信号；数字信号处理；频谱；可变参数；数字均衡器

 引言
    随着现代声频技术日新月异的发展，人们欣赏音乐的水平在不断提高，对录音师的录制水平的要求也越来越高。在现代音乐的录制过程中，录音师会运用各种各样的均衡器、压缩限幅器、混响器等设备进行声音处理，从而获得令人满意的高保真重放。在如此众多的声处理设备中，均衡器可以说是使用最多的声处理设备。音乐信号包括基波和谐波，基波的高低决定音调，而音色则由谐波的结构决定，在实际使用中，人们主要借助均衡器来调整信号带宽内不同频段成分的相对大小，从而改变基波与谐波之间的对应关系，使音色发生一定的变化，改善声音的音质。如对底鼓适当提升80 Hz左右的频率，可以使声音听上去更加丰满；而对贝斯可衰减60 Hz以下无频率信息的频段，而提升100 Hz左右，以提高力度；对于铜管乐器，可提升5 kHz左右的频率，以提高穿透感等。
    均衡技术已有70多年的历史，最初的均衡器都是基于模拟信号的，随着数字信号处理技术的发展和提高，出现了数字均衡器。目前，数字均衡技术主要应用于计算机音频处理、媒体播放器以及专业音响设备等。本文对音乐信号进行频域均衡处理的一阶、二阶可变参数数字均衡器的设计进行研究，利用Matlab软件编写程序对所设计的均衡器进行频率特性分析，讨论参数变化对均衡器性能的影响，对实际的音乐信号进行均衡处理，并对均衡效果进行分析。

1 可变参数数字均衡器的模型
    均衡器利用滤波器的原理，调整信号带宽内不同频段成分的相对大小。对音乐信号作不同处理所需要的均衡器频响特性也就不同，因此均衡器的设计归结为不同频响特性滤波器的设计。
    一阶可调均衡器由一个一阶低通滤波器和一个一阶高通滤波器构成，它们的传递函数分别为：
 
    上面两个滤波器组合，如果低频输出乘以K与高频输出相加，就构成低频均衡器，如图1所示，其传递函数为：
   

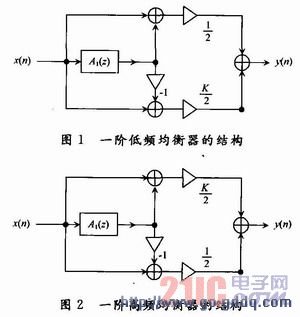
    若把高频输出乘以K与低频输出相加，就构成高频均衡滤波器，如图2所示，其传递函数为：
   
    式中：K是一个正常数，控制低频或高频幅度增强或减弱的量；a和K均为一阶可调均衡器的可变参数。
    二阶可调均衡器由一个二阶带通和一个二阶带阻滤波器组成，其传递函数分别为：
 
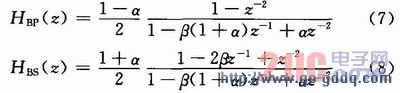
    带通滤波器的中心频率w0和带阻的陷波频率w0通过下式由β控制：
 
    而这两个传输函数的3 dB带宽Bw通过下式由α控制：
 
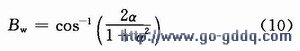
    这两种滤波器复合，其传递函数为：
 

[1] [2] [3] [4]  下一页