·上一文章：基于Linux操作系统的射频识别安检设计方案
·下一文章：电磁流量计在石油化工中应用
2.2RBF神经网络原理
RBF网络是一种典型的局部逼近神经网络，它不像全局逼近神经网络那样，对每个输入输出数据对、每一个权值均需要调整，而是调整对输出有影响的少量几个权值，从而使局部逼近网络在逼近能力和学习速度方面有明显的优势［5］。
该RBF网络结构为8－20－1形式。输入层8个节点只是传递输入信号到隐层，隐层20个单元通过径向基函数实现变换后输出到输出层。输出层节点只是简单的线性函数。最常用的径向基函数是高斯核函数(Gaussian kernel function),如式(1)所示。
其中，uj是j个隐层节点的输出，X＝（x1，x2，…，xn)T是输入样本，Tj是高斯函数的中心值，σj是标准化常数，即径向基宽度，M是隐层节点数。节点的输出范围在0和1之间，且输入样本越靠近节点的中心，输出值越大。
网络的输出yi为隐层节点输出uj的线性组合，如式(2)所示。
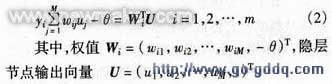
2.3训练方法
由式(1)可知，该网络要学习的参数有3类：RBF的中心、宽度和连接权重。可以分别训练，也可同时进行。在隐节点数确定的情况下，采用遗传算法同时训练中心Tj、宽度σj以及隐层与输出层的连接权重Wij。
遗传算法是模拟生物进化过程的计算模型。它对包含可能解的群体反复使用选择、交叉和变异操作，不断生成新的群体，使种群不断进化。当输入节点较多时，该算法比传统BP算法的全局最优性更佳，速度更快［6］。算法的适应度函数见式(3)。
其中，N为样本数量，M为隐层节点数，b为待定系数(一般取较大的值，以保证适应度大于零)，d为期望的输出，y为网络的实际输出。 
择概率S(j)见式(4)。其中，fj表示个体j的适应度。S为群体规模。
文中采用单点交叉，将两个基因串对应交叉位的值相结合生成新的基因串。
重复选择交叉和变异操作，直到网络达到精度要求。
