·上一文章：录音电子门铃电路
·下一文章：基于GPRS传输的输电线路红外测温系统
2 FIR滤波器的FPGA实现
由式(4)可知，FIR滤波器的数学表达式就是卷积运算，也就是做乘加运算。例如，一个M阶的FIR滤波器的输出是输入样本的M个依次值的加权和，加权系数就是此滤波器的单位冲激响应值。对于上节设计的10阶线性FIR滤波器，可以得到：
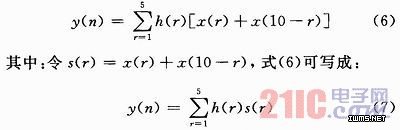
这样，10阶FIR滤波器的结构可以描述为：输入样本x(n)经过10阶移位寄存器延迟后得到10个具有不同延迟的抽头，将对称的抽头值相加后再与相应的权系数相乘，5个乘积相加就得到滤波器的输出值。滤波器结构如图1所示。
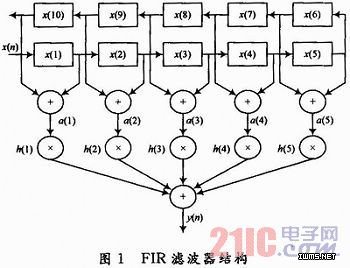
滤波器抽头与权系数之间存在着乘法运算，在硬件实现中乘法运算是相当复杂的运算，不仅占用大量硬件资源，而且运算速度较慢。为了提高运算速度，在此利用FPGA逻辑单元(LE)中的查找表实现替代乘法运算的查表运算。为了说明方便，在此以4阶滤波器为例，数据为2位的二进制整形。设a(1)=01，a(2)=11，h(1)=10，h(2)=01，权系数与抽头之间的乘加运算如图2所示。
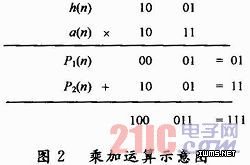
图2中，P1(n)为抽头低位与权系数的乘积结果，P2(n)为抽头高位与权系数的乘积结果，在此称之为单位积。常规的计算顺序是先将P1(n)和P2(n)的对应项在垂直方向上移位相加，所得结果再进行水平方向上相加。但是从图中可以看出，先将P1(n)和P2(n)在水平方向上相加，然后再进行垂直方向上移位相加，所得的结果是一样的。第二种顺序中，P1(n)和P2(n)是h(n)和a(n)的某个比特位的乘积，而对于设计好的FIR滤波器h(n)是固定的，这样就可以通过a(n)某比特位的组合来查表求出P1(n)或P2(n)，并在水平方向上实现求和。如表1所示，a1(n)表示a(n)的低位组合，单位积P1表示相应的权系数和。
