2．2 改进的二阶相位扰动法
    二阶相位扰动法在研究普通相位扰动法的基础上形成，该方法中，扰动序列是由两个独立同分布的随机序列相加产生。具体的原理结构，如图3所示。

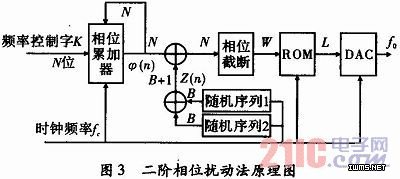
    如图3所示，两个B位独立同分布的随机序列相加生成B+1位的扰动序列，然后由B+1位的扰动序列扰动原始输出φ(n)，这样能获得更好的杂散抑制效果。
    对于二阶相位扰动，需要考虑量化噪声的三阶矩成分E{&epSILon;3(n)}，此时的输出信号泰勒级数展开式为
   
    假设扰动序列为在[0，△]上服从均匀分布的两随机序列之和，则扰动序列的概率密度为
   
    将满足式(14)的扰动序列加在相位序列上，并且截断为W位，由此产生的总量化噪声有3种情况

    从式(17)可知，采用二阶相位扰动法，杂散分量的抑制可达每相位位18 dB，相比普通相位扰动法性能有很大改善。

3 仿真验证
    利用嵌入到Matlab中的DSP Builder工具进行仿真，具体的模型如图4所示。仿真参数：时钟频率fc=1 MHz；频率控制字K=485 952；相位累加器位数N=22；相位寻址位数W=4；ROM输出位数L=20；取两个独立的24级18位输出m序列之和作为扰动序列。仿真结果送到Matlab的工作空间并进行功率谱变换，从而验证系统的设计。

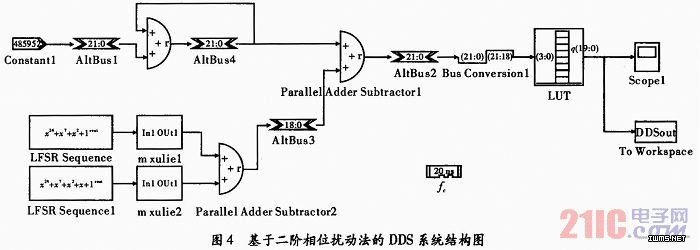
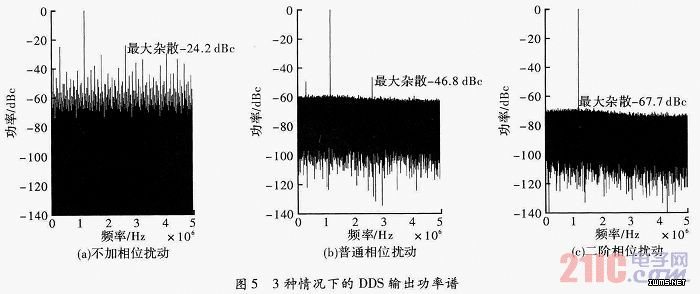
    图5是将3种情况下的DDS系统仿真结果进行归一化功率谱变换得到的图形。其中图5(a)表示不加任何相位扰动的系统输出功率谱。图5(b)表示加入一个24级18位输出m序列作为扰动序列后的系统输出功率谱。图5(c)表示取两个24级18位输出的m序列之和作为扰动序列，这种情况下的系统输出功率谱。从图中可以看出，由于相位寻址位数为4，不加相位扰动时的最大杂散为-24．2 dBc，普通相位扰动时为-46．8 dBc，而二阶相位扰动时减小到-67．7 dBc，这和理论推导的-72 dBc有误差，是因为在进行FFT时点数限制的影响。从以上数据可以得出：使用二阶相位扰动法，DDS的杂散抑制性能得到较大地改善。

4 结束语
    在研究基本相位扰动法的基础上，提出了一种新的二阶相位扰动法，该方法可使杂散分量的抑制达到每相位位18 dB。因此在同样杂散精度的要求下，使用该方法的设计可以减少ROM寻址的位数，压缩ROM的存储空间，降低硬件的设计复杂度和产品成本。

上一页  [1] [2] [3]