·上一文章：基于FPGA的FIR数字滤波器的优化设计
·下一文章：战场复杂电磁环境视景仿真研究
1．2 矩量法
自从20世纪60年代Harrington提出矩量法基本概念以来，它在理论上日臻完善，并广泛用于工程之中，特别是在电磁兼容领域，矩量法更显示出其独特的优越性。它的思想是将待求的积分或微分问题转化为一个矩阵方程问题，借助于计算机，求得其数解。很多电磁场问题都归结为这样一个算子方程：
式中：L为算子；g为已知激励函数；f为未知响应函数。展开未知函数f为有限个线性无关的已知简单函数fn之和：
式中：an是展开系数；f1，f2，…，fn为展开函数或基函数。将式(8)代入式(7)，再应用算子L的线性，可以得到：
选一组线性无关的函数ωm(m=1，2，…，N)，分别与式(9)两边作内积。
因为m=1，2，…，N，所以得到N个方程，解出f。
矩量法就是这样一种将算子方程转化为矩阵方程的一种离散方法。
矩量法更适合于求解具有表面电流分布的各种几何体，如计算天线远、近场辐射场强、方向图等。它的算法简单，不需要设置边界条件，而且对于适当的尺寸，求解速度较快。
1．3 时域有限差分法
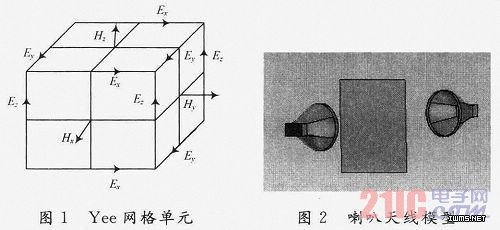
K．S．Yee于1966年提出求解电磁问题的时域有限差分法，其原理非常简单，即直接将时域Maxwell方程组的两个旋度方程中关于空间变量和时间变量的偏导数用差商近似，从而转换为离散网络节点上的时域有限差分方程。
为了建立差分方程，首先要将求解空间离散化。通常是以一定形式的网格来划分求解空间，Yee提出了如图1所示的差分网格单元，其特点是在同一网格中，E和H的各分量在空间取值点交叉放置，使每个坐标面上的
的四周由
分量环绕，同时每个场四周由场环绕。这样，配置符合Maxwell方程的基本要求，也符合电磁波空间的传播规律，使电磁波的时域特性被直接反映出来，直接给出非常丰富的电磁场问题的时域信息。
时域有限差分法在天线辐射特性计算、微波电路分析、散射体雷达散射截面等方面有广泛的应用，对于计算孔缝对屏蔽效能的影响具有优越性。
