摘要：提出采用正则有符号数字量(CSD)编码技术实现FIR滤波器。首先分析了FIR数字滤波器理论及常用设计方法的不足，然后介绍了二进制数的CSD编码技术及其特点，给出了其于CSD编码的定点常系数FIR滤波器设计过程，使用VHDL语言实现了该常系数滤波器的行为描述。最后在Max+PlusⅡ环境下进行实验仿真和验证，与DA和2C编码算法比较结果表明，用CSD编码技术实现的滤波器可以有效提高运算速度并降低FPGA芯片的面积占用。
关键词：CSD编码；分布式算法；FIR；FPGA；常系数乘法

    引言
    在图像处理、语音识别等数字信号处理中，数字滤波器占有重要的地位，其性能对系统有直接的影响。随着系统在宽带、高速、实时信号处理上要求的提高，对滤波器的处理速度、性能等也提出更高的要求。目前数字滤波器的硬件实现方法通常采用专用DSP芯片或FPGA，DSP特有的一些硬件结构和特性使其非常适合作数字滤波电路，但由于其软件算法在执行时的串行性，限制了它在高速和实时系统中的应。FPGA最明显的优势在于其实现数字信号处理算法的并行性，可以显著提高滤波器的数据吞吐率，随着FPGA技术的不断发展，现在的FPGA不仅包含查找表、寄存器、多路复用器、分布式块存储器，而且还嵌入专用的快速加法器、乘法器和输入／输出设备，因而成为高性能数字信号处理的理想器件。而在FPGA中，数字滤波器不同的实现方法所消耗的FPGA资源是不同的，且对滤波器的性能影响也有较大差异。基于此，本文从FIR滤波器的系数考虑，采用CSD编码，对FIR数字滤波器进行优化设计。

    1 FIR滤波器的基本原理
    一个L阶的FIR数字滤波器的基本系统函数见式(1)：
   
    式中：h(n)表示滤波器的系数；x(i)表示带有时间延迟的输入序列，此表达式对应的直接型实现结构可用图1来表示。

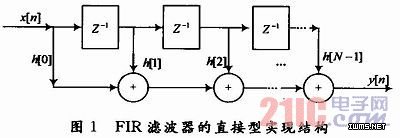
    可以看出，FIR滤波器是由一个“抽头延迟线”加法器和乘法器的集合构成的。传给每个乘法器的操作数就是一个FIR系数。对每次采样x(n)要进行N次连续的乘法和(N-1)次加法操作，因实际中滤波器的阶数都很高，实现高数据吞吐率就需要很多的硬件乘法器，硬件实现时将占用大量的资源，同时也会因此影响滤波器的速度和性能。为了解决这个问题，人们从多个角度寻求优化方法。从数字滤波器表达式看，对它
的优化操作，实际最终转换成两类改进。一类是针对输入xi的DA操作的改进；另一类是针对系数hi编码的操作。

    2 DA算法
    分布式算法(Distributed ArithmetIC，DA)是为了解决乘法资源问题而提出的经典优化算法这种算法结构，可以有效地将乘法运算转换成基于查找表LUT(Look Up Table)的加法运算，利用查表方法快速得到部分积。
    对于低阶而言，由于LUT表地址空间较小，与传统算法相比，分布式算法可极大地减少硬件电路的规模，提高电路的执行速度。然而当FIR滤波器阶数很高时，作为查找表的ROM将很大。阶数每增加1位，ROM容量就增加1倍，这种以2的幂次递增的资源占用是硬件资源不可接受的。因而在滤波器系数较高时，为了减小查找表的规模，常采用一定的方法将大LUT分割为一些小的LUT的方法。如滤波器的多相分解结构、多路复用器和加法器替代查找表的算法等。

    3 CSD编码算法
    常数乘法可以通过“移位-加”来完成，而乘数中“1”的个数决定了“加”操作的次数，当然“1”的个数越少越好，正则有符号数字量CSD(CANonic Signed Digit)编码就可以实现“1”的个数的最小化。
    3．1 CSD编码
    与传统的二进制编码的二值表示法不同，CSD编码的数字值域为0，1和-1。-1常表示成1。这种编码是具有最少非零元素的一种表示法，用CSD编码表示数字的形式具有惟一性。在实际硬件电路中可以采用如下原则生成最佳CSD编码：
    ①从最低有效位开始，用10…0 取代所有大于2的1序列，此外还需要用110 取代1011；
    ②从最高有效位开始，用011代替10 。
    最佳CSD编码的特点是：
    ①在一个CSD数据里，没有两个连续的非零位；
    ②对同一个数字的CSD编码是独一无二的；
    ③是数字表示法里，所含非零位数最少，相比于二进制补码系统平均减少33％的非零项。

[1] [2] [3] [4]  下一页