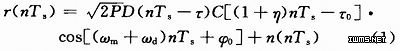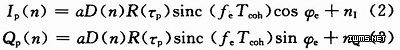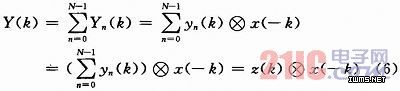摘要:弱信号环境下快速有效的C/A码捕获算法,在高灵敏度GPS接收机中占据着重要地位,同时也是高灵敏度GPS接收机实用化的关键。通过对捕获信号相关幅值的统计特性分析,从理论上揭示了微弱GPS信号难于捕获的根本原因,并论述了当前主要的数据累积方法的利弊。通过对GPS系统和导航电文格式的分析,将快速相干累积与卫星位置预测相结合提出了新的GPS微弱信号捕获算法。理论分析和仿真结果表明了本算法的可行性,在信噪比SNR为-43 dB时可以稳定地捕获GPS信号。使用实际数据测试表明,该算法能明显增加捕获到的卫星数量。
关键词:全球卫星定位系统;微弱信号捕获;帧同步码;相干累积
引言
当前GPS作为全球性卫星导航系统的应用范围越来越广,而其在弱信号环境下的接收技术研究,受到紧急救援和未来军事需求的刺激已经成为研究热点。其中,高灵敏度接收技术在GPS接收机中的应用,由于不受环境和条件的限制尤为受到重视。在高灵敏度GPS接收机中,由于捕获算法处在基带处理的最前端,因此高效的微弱GPS信号捕获算法是提高高灵敏度GPS接收机性能的关键。通常的弱信号环境比室外信号强
度低约20~30 dB,载噪比小于28 dB-Hz,故被视为弱信号,高灵敏度GPS接收机主要通过信号处理算法来获得高的信号处理增益。本文分析了主要信号累积技术的优缺点,讨论了弱信号环境下GPS信号检测值的概率统计分布特性,在此基础上结合快速相干累积算法,提出了利用帧同步信息的微弱GPS信号捕获算法,并分析了其可行性。通过仿真验证和实际数据测试,证明算法可行有效。
1 GPS信号模型及特性
实际到达接收机的中频数字信号中包含着L1及L2载波的完整信息,在弱信号的C/A码捕获研究中,忽略P码及L2载波进行分析,可采用下式:
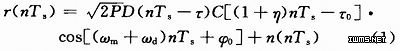
式中:
/2011.08/15/e.jpg)
为信号幅值;D(·)为数据位;τ为数据位延迟;C(·)为PRN码;η为码速率多普勒变化率;τ0为输入信号的码相位延迟;ωm为载波标称频率;ωd为载波多普勒频移;φ0为载波初始相位;n(·)为等效输入的带限白噪声。
按照基本的捕获流程,接收的数字中频信号经过载波剥离和C/A码进行相关,再进行相干累积和非相干累积后输出一个幅值V,当幅值V超过预定的捕获门限时判决捕获成功。其中,信号经过相干累积后I,Q支路可表示为:
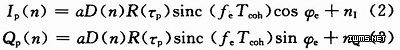
式中:a为信号的幅值;τp为本地搜索C/A码与接收C/A码之间的相位差;fe为接收载波与本地载波之间的频率差;φe为两载波之间的相位差;Tcoh为相干累积时长;nI和nQ分别代表I支路和Q支路上的噪声,其功率σn2为:

即噪声功率与相干累积时长成反比,从一个方面揭示了弱信号捕获算法中,相干累积能提高信噪比的原因。
理论上捕获门限可以根据虚警概率和信号检测幅值概率的分布关系,计算出理论上的捕获门限,但由于实际当中信号检测幅值的概率分布关系相当复杂,因而实际当中对捕获门限很少根据理论进行设置,而是通过相对捕获门限来完成捕获判决。
根据捕获幅值的统计特性可知,在弱GPS信号环境下根据单次的捕获结果进行门限判决,产生误判的概率非常大。如果对多次捕获的结果进行统计比较,进行相对捕获判决就可以克服这种不足,从而提高捕获算法性能。
2 信号累积算法性能分析
在微弱GPS信号捕获算法中,信号累积技术是提高处理增益的关键。当前提高信号处理增益的基本方法为信号累积技术,可分为三类:相干累积、非相干累积和差分累积。其中,信号经相干累积处理获取的增益效果最佳,但应用受到导航数据比特翻转的限制,如累积过程中遇到数据比特翻转性能会有所下降;非相干累积和差分累积的提出就是为了克服和减少这种影响,但需付出不同程度的信噪比损失作为代价,并且原始信号越差,它们的信噪比损失越大,因此只能与相干累积结合使用。目前微弱GPS信号的捕获算法均是以信号累积理论为基础,如半比特捕获算法和全比特捕获算法,通过估计数据比特跳变来进行长相干累积的捕获算法,以及在对三种数据累积技术分析比较的基础上提出相干累积与差分检测相结合的方法等,这些算法的改进均是为了提高对微弱GPS信号的捕获性能,使高灵敏度GPS接收机实用化。因而,在此尽量延长相干累积的时间,从而最大限度地提高信号的处理增益,捕获更加微弱的GPS信号。
2.1 新的快速相干累积算法
前面提到的相干累积算法,通常是将每1 ms的相关运算结果进行相干叠加运算,即进行多少次相干累积,便进行多少次相关运算。即便采用FFT算法,相关运算的运算量依然很大。在微弱GPS信号的捕获过程中,通常需要进行长时间的相干累积运算,以提高信号处理增益,因此这里采用文献提到的方法,先将信号进行叠加,再进行相关运算的方法来减少运算量。基本原理如下:
已知相关运算的卷积形式表达为:
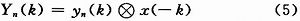
式中:Yn(k)为第n次的相关值;yn(k)为第n毫秒接收到的原始中频数据;x(k)为本地C/A码与本地载波的组合,则N次相干累积的表示式为:
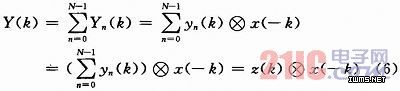
式中:z(k)为N段信号的累积。可见,经过变换后进行N次相干累积只需做1次相关运算,运算量减少近N倍。
[1] [2] [3] [4] 下一页