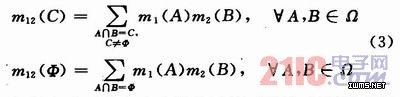2．1．2 Sment改进方法
    1990年，Sment提出了另一种改进方法，将冲突全部赋予空集。改进后得合成公式为：
   
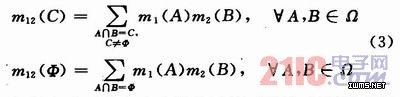
    但是上述两种方法改进效果并不明显，仍然没有解决“一票否决”的现象。
2．1．3 孙全改进方法
    针对上述问题，孙全在2000年提出了加权形式的组合公式，并引入证据间两两冲突程度参数K，证据可信度参数&epSILon;和证据平均支持度q(A)。这其实是一种新的证据可信度分配冲突的方法。他提出的合成公式如下：
   
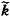
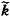
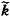
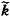
    式中：式n个证据集中每对证据集总和的平均，它反映了证据两两之间的冲突程度；ε是的减函数，反映了证据的可信度，也就是当证据之间的冲突增大时，证据的可信度将降低；与D-S理论中的K不同，K反映证据总体上的冲突程度，当K增大时，不一定增大。
    式(4)又可以写成如下形式：
   
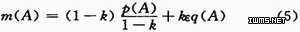
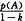
    从式(5)可以发现其中第一项的正是D-S证据组合公式。因此上式实际上是一个加权和的形式，当K较小时，即证据冲突较小第一项起主要作用，合成结果近似于D-S合成结果。当K=0，等同。当K=1时，即证据高度冲突时，合成结果主要由第二项εq(A)决定，即由证据可信度及证据对A的平均支持度决定。m(X)中第三项表现了当冲突K增大或证据可信度ε减小时，都会使未知程度增加。这些表达都是较合理的。
2．2 对融合模型进行改进
    上述方法主要是基于对D-S证据理论中组合规则的改进，还可对融合模型进行改进。Murphy于2000年就已经提出了组合前平均证据的方法。Murphy的方法就是一种修改模型而不变Dempster规则的方法。Murphy分析了已有的改进方法，提出了一种证据平均组合规则，具体的步骤是：首先将证据的基本概率指派进行平均，之后再用Dempster组合规则进行信息融合。与其他的方法比较，该组合规则可以处理冲突数据，且收敛速度较快。但是Murphy的平均方法只是将多源信息进行简单的平均，没有考虑各个证据之间的相互关联。
    2004年，邓勇对Murphy平均法作了改进，在Murphy方法的基础上，引入一个度量证据体间相似程度的距离函数，并进一步获得系统中各个证据被其他证据所支持的程度，将该支持度作为证据的权重，对多源证据进行加权平均后再利用Dempster组合规则融合证据信息。该方法继承了Murphy方法的所有优点，并且具有更强的抗干扰能力，收敛速度更快。其简要步骤如下：
    首先，得到各个证据之间距离矩阵DM，矩阵元素dij代表证据i和证据j之间的距离，即：
   

上一页  [1] [2] [3]  下一页