然后，得到证据之间的相似程度矩阵SM(矩阵元素为smij)和各证据的支持度Sup(mi)，即：
   
   
3 算法验证和结果分析
    设有5个证据如表1所示。m(A)，m(B)和m(C)表示各个证据对识别目标A，B和C的BPA。对于目标A，2号证据对它的指派为0，其他证据对它的指派都较高。尤其是最后3个证据，对它的指派都是一样的。对于目标B，只有2号证据对它的指派非常高。正常推断最后结果应该是A。

    使用D-S方法和上述各改进方法对表1数据进行融合的结果见表2。由于2号证据对A目标的BPA为0，无论其他证据对A的支持程度有多高，经典D-S方法的最后融合结果A的概率均为0。仅仅由于证据2对目标B的支持率高，虽然其他证据对它的支持率都不高，最后的融合结果却是B。这是典型的失效问题。

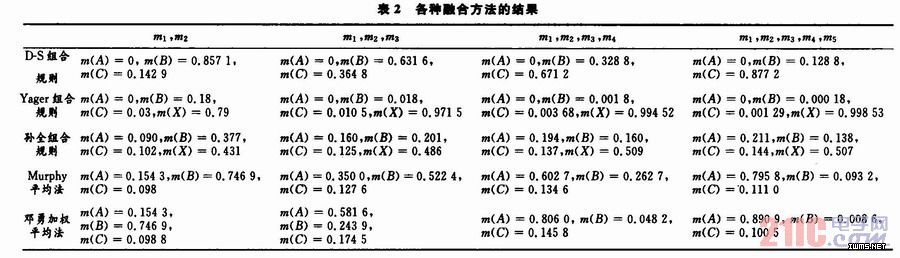
    Yager的结果中，不论以后收集多少支持A的证据，未知项m(X)的数值始终在增加。孙全对Yager的改进方法可以部分克服原方法的缺点，表2中可以看出，随着支持A的证据越来越多，m(A)的数值有所增加，但是增加速度很慢，且未知项m(X)的数值没有明显降低，系统无法作出决策。随着证据的增多，Murphy的平均方法和邓勇加权方法都能正确的识别出目标A。但是由于Murphy没有考虑证据之间的相关性，在系统收集到4个证据时，Murphy方法才识别出目标A(对应表中的m1，m2，m3，m4列)。邓勇加权的方法在收集到第3个证据时就可以正确识别目标(对应表中的m1，m2，m3列)。分析其原因可以发现：由于传感器本身不可靠或是敌人的干扰或是环境恶劣等因素，导致证据2与实际情况有较大的偏差，Murphy通过将证据进行平均以“抵消”这一“坏值”的影响。但是由于Murphy的方法只是对证据简单平均，在某些情况下(如本例中m2(B)=0.9，也就是m2强烈支持目标为B，系统需要更多的证据才能有效“抵消”收集的“坏值”。而邓勇加权方法考虑了证据之间的相互关联的特性，考虑了各个证据的有效性，有效地降低了“坏值”对最终融合结果的影响，使得在比较少的证据下就能使结果收敛为正确的目标。

4 结语
    不确定信息的表示和若干个信息的综合是不确定性推理的主要问题，D-S证据理论为不确定信息的表示提供了一个很好的框架，其组合规则在大多数情况下是合理的。但是由于人为或自然环境等因素，信息融合系统中收集的证据常常有较大的冲突，这时使用传统的Dempster组合规则无法有效地处理这些冲突证据。本文总结分析了相关的国内外典型文献的改进思想，并进行系统条理的分析，为证据理论的发展和改进提供了有价值的参考，并为证据理论在不确定性推理方法奠定了良好的基础。

上一页  [1] [2] [3]