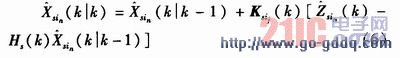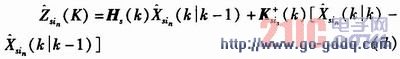这样一来，一个可能的划分是把集合Z划分成两个与目标互联的测量子集Zt和没有与其他目标互联的虚拟测量子集Zf，表示为γ={Zt，Zf}，其中，Zt={Zj1j2j3}，ji=1，2，3，…，ni，i=1，2，3；Zf={Ziji}，ji=1，2，3，…，ni，i=1，2，3；γ={Zt，Zf}表示集合Z划分成子集Zt，Zf的可能，把集合分成测量子集和虚拟测量子集；在静态传感器测量数据互联中，对一个位置进行全面测量估计至少需要两个传感器；否则就是认为虚拟测量子集。因此，测量集合Z的最佳关联划分是把Z划分为来源于目标的测量子集Zt和虚警子集Zf，这时只需求解γ与γ0的最大联合似然函数比，即

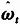
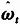
    真实目标位置ωt近似于极大化广义似然比的极大似然估算值，所以式(4)中的ωt可用代替，该估算值可从3个传感器测量获得，即
   

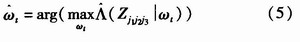
2 近似测量
    近似测量算法采用节点状态估算推导形成，节点状态估算算法为

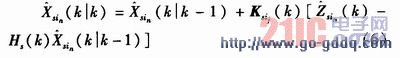
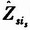
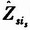
    式中，为局部节点s用于更新第i个局部轨迹的近似测量；Ksis(k)是局部节点s的第is个局部轨迹的滤波增益。根据式(6)求解有

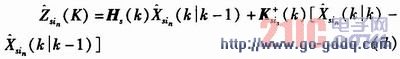
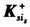
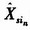
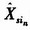
    式中，(k)是Ksij(k)的逆阵或伪逆阵。局部节点仅向融合中心传送状态估计值，不传送近似测量值，通过式(7)可以在融合中心获得局部Zigbee节点的近似测量值。近似测量构造要求信息融合中心已知轨迹状态值(k|k-1)、状态估计值(k|k)。增益矩阵Ksij(k)和测量矩阵Hs(k)之所以可作为近似测量，是因为构造的结果可能不是实际测量值，这取决于局部节点使用的数据关联算法。当局部节点使用最近邻域互联算法时，所构成的测量值是局部近似算法中使用的实际测量值；但当局部节点使用联合概率数据为互联算法(JPDA)或混合归并(MR)算法时，重新构成的算法结果不产生实际测量值；因而原测量值需要加权平均。N≥3时多节点分配方法适用于各节点公共监视区的轨迹关联校验。对各局部节点间的局部公共区则要利用N=2时的各种轨迹关联算法或使用二维分配模型求解。

    3 结束语
    在多数目标跟踪的应用中，获得大量精确的传感器数据较困难。例如：Zigbee无线车辆门禁控制系统中，只能每几秒钟测量一次小区门前内外机动车的位置，当获取的信息不足时，所采用的模型的精度就显得尤为重要。原因有二：第一如果控制系统对目标状态的采集频率高于Zigbee传感器的频率，那么就要用到跟踪器对位置的预测值，不同的模型对这个预测值的质量影响很大；第二是为了优化Zigbee传感器的性能，必须最大限度地利用来自传感器的有限数据，在多数近似测量算法中，只能通过开发一些精度的实用模型来实现。上述节点状态估算算法有效地改善了Zigbee传感器的性能，提高了跟踪精度。

上一页  [1] [2]