·上一文章：通过I2C兼容接口读取ADC数据
·下一文章：智能管道关键技术分析
从前面几种编码可以看出，所使用的方法都是水平校验加其他一种校验共同构成双容错。不同之处就在于“另一种校验”的不同选择。如将另一校验盘上的校验元看作一个“0”、“1”向量，每块数据盘上的单元对这些校验元的影响可用一个“0”、“1”矩阵来表示。如表5中的第1列的4个数据单元对Disk7中的各校验元的影响可表示为如图4所示矩阵。
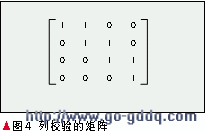
在这种表示下，前面所说的更新复杂度就对应着矩阵中1的个数。于是构造一个双容错阵列码的问题就转变为：寻找若干个这样的矩阵，使得其中1的个数尽量少，并且任意2个之和为满秩。
在p为素数时，文献[7]中构造的Liberation码使得p×p阶矩阵1的数目不超过p+1，其构造的p个矩阵可简单地描述为：各对角线加一个额外单元。第k个矩阵的额外的1单元的位置可描述为(k(p-1)/2 Mod p,1+k(p=1)/2 Mod p)。得到的编码如表6所示。
3.4 PDHLatin码
前面这些编码为MDS码的充要条件均为：码长与素数相关(RDP为p+1，其他为p+2)。它们的双容错解码方法均为根据一个已知单元，然后通过校验关系与失效单元形成的链式关系依次恢复所有单元。这使人们理解到其容错能力的本质是任意两列都可以形成这样的关联结构。文献[8]中利用拉丁方构造了PDHLatin码，使得码长不再必须关联一个素数。
所谓拉丁方是指n×n的方阵中填入n个不同符号，使得每行每列的符号都不重复。显然拉丁方的每两列构成一个n元置换。所谓汉密尔顿拉丁方是指拉丁方的任何两列构成的置换为单环的。图5为一个9阶汉密尔顿拉丁方。
从一个给定的汉密尔顿拉丁方，我们可以用与EVENODD码类似的方法构造编码，只不过各单元对于第二校验盘的校验关系不再依单元所在对角线位置决定，而是根据拉丁方相应位置的符号决定。根据图5，得到表7所示的PDHLatin码。
3.5 X码
上面介绍的几种编码方法虽然都达到了冗余的最优，但在更新复杂度方面均稍高于最优值，那么是否可以达到两者同时最优呢?文献[9]提出的X码是一种这样的双容错编码。
X码的想法也很简单，仍然是在阵列中采用主对角线和辅对角线两种校验，但是通过巧妙地将校验单元分布到各个磁盘中(而不是像其他方法中，校验单元被分离出来，独立存放于校验盘)，使得系统同时达到了两方面指标同时最优。
为了满足双容错的要求，X码也要求阵列中包含的列数(或说码长)为素数。码长为素数p的X码中，每一列包含p-2个用户数据单元，2个冗余校验单元。
3.6 B码
是否还存在与X码相同特性的其他编码方案呢?显然将两个X码阵列重叠，系统仍然保持最优冗余与最优更新复杂度。
这样得到的新编码，在磁盘数目不变的情况下，每块盘需要关联的单元数目加倍。而在实际中，为了简化实现，我们实际上需要每块盘关联的单元数目尽量少。对于n块磁盘，在保持最优冗余与最优更新复杂度的条件下，每块盘最少需要多少个单元来关联校验呢?文献[10]提出的B码在双容错的情况下很好地解决了这一问题。
通过将编码构造等同于图论中的完全图完美-因子分解问题。并根据图论已有的结论，给出一种各方面性能均达到最优的编码。依据一个完全图的一种完美1因子分解方案，我们可以构造如表8所示的双容错编码——B码。
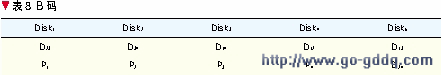
这种编码，每块磁盘包含至多1个校验单元，并且只有一块磁盘不包含校验单元。它将n个符号的所有2元组分划为多列，并且满足双容错要求，因而在保持了最优冗余度与更新复杂度的前提下，码长达到最长。因而这种编码也被称做最长最低密度阵列码。
