1 存储容错编码评价指标

　　近20年来，随着计算机技术的迅猛发展，大规模存储系统的发展也十分迅速。当前，普通PC机的存储器的容量已经达到了太比特级别，这较之20年前的20 MB存储容量提高了10 000倍。

　　除了传统的磁盘驱动器之外，新型的固态存储(SSD)存储器也已经走向市场。尽管单个存储器的容量发展迅速，但是却仍然赶不上人们对存储容量需求的增长速度。

　　随着大型计算机系统由“以计算为中心”向着“以信息处理为中心”的转变，以及信息量的爆炸式增长，人们对海量存储系统的需求日益提高。海量存储系统本质上是将很多的单个存储器件(下面均以磁盘为例)，通过系统的接口，连接整合为一个虚拟的容量巨大的单一存储器，即磁盘阵列。

　　随着阵列中磁盘数目的增多，系统的可靠性也随之下降。工业界一般使用平均数据丢失时间(MTTDL)来衡量阵列的可靠性。

　　设单个磁盘的平均失效时间为MTTFdisk，则对于包含n块磁盘的无冗余阵列来说，其MTTDL可简单估计为：MTTDL=MTTFdisk/n。可见，当n较大时，整个系统的可靠性将成比例下降。这对于较大规模的系统来说是不可接受的。利用冗余数据编码来提高系统可靠性是公认的解决这一问题的较好方法。通过巧妙地将m块标准大小的磁盘上的数据，增加部分冗余校验信息，编码后存放于n块磁盘上，使得系统满足：对于任意k块磁盘失效，都可以通过其他n-k块未失效盘中的数据解码恢复，则称整个系统是k容错的，或者称k为系统的容错数。

　　分析表明[1]，对于k容错的系统来说，可以近似估计为：

　　因而，在大规模系统中，容错数可以说是另一种对系统可靠性的描述方式。市场中一般磁盘的MTTFdisk为105左右，系统修复时间MTTR一般为10左右。根据(1)式可以看出，当系统磁盘数为103～104时，一般2容错或是3容错编码就基本上可以满足存储系统的容错要求。

　　系统用于增加容错能力而添加的冗余越多，系统的额外造价也将越高。因而在具有相同容错数的前提下，人们往往追求更小的冗余度，即(n-m)/n的值，其中n为系统磁盘数、m为存储用户数据的磁盘数。根据编码理论的Singleton界，k容错系统的最小冗余度为：k/n。达到这一最小值的编码方法称做MDS码。目前多数存储编码研究都集中于构造不同参数下的MDS码。

　　除了上述指标，任何计算机系统的速度与效率永远是需要考量的重要指标。这里我们不讨论如何有效地并行处理多磁盘中的数据读取(那是另外一个较大的课题)，而着重研究由于冗余编码带来的额外计算开销。对于即便是相同的编码方法，由于编/解码算法的不同，可能计算效率的差异较大。由于在计算机系统中，最终的编码运算都会反映为一些二进制运算，因而研究者通常使用编码需要的总的二进制异或运算次数来衡量由于额外冗余编码带来的系统计算开销。对于一个随机存取的存储系统来说，随机小块信息写操作的性能尤为重要。编码运算中每个单元所参与的平均异或次数可以用来衡量这一指标，我们称其为编码的更新复杂度。

　　综合上面讨论，存储系统容错编码问题可以归结为寻求对如下指标进行优化的编码方法

　　系统满足需要的容错性能，容错数为k的系统。

　　系统有较小(或最优)的冗余度

　　系统有较小(或最优)的编码/更新复杂度。

　　2 线性编码

　　对于单容错系统来说，简单的奇偶校验即可使得上面的3个指标达到最优。经典的系统都是使用的这种方法。然而对于k大于1的情况，问题的解决就不是那么简单了。从通信编码理论的丰富成果中，两种比较有代表性的编码方法被人们挑选出来，并用于解决存储容错问题，他们是二进制线性码和RS码。

　　2.1 多维阵列码

　　图1所示是二维阵列编码及校验矩阵。二维阵列码是奇偶校验的自然推广，由图1很容易看出它是双容错的。二维阵列码保持了单容错时奇偶校验码的最优编码复杂度的特性，但是二维阵列码的冗余度不再是最优的了。

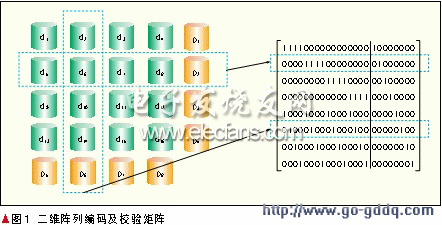
　　二维阵列码也很容易推广为k维阵列。并且容易得到这样编码的k容错特性。但是随着k的增大，冗余会越来越大[2-3]。

　　2.2 Full码

　　图2所示是FULL-2码。FULL-2码可看做是二维阵列码的推广。

　　FULL码依然保持了最优的编码复杂度，并且冗余度要比阵列码好很多。然而不幸的是，当k大于3时，FULL-k码不再是k容错的[4]。

[1] [2] [3] [4]  下一页