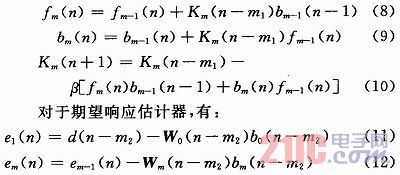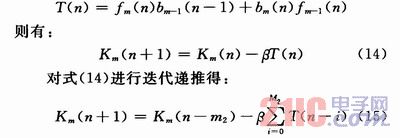2 改进型RD-GALJP算法
由于GALJP的算法相对复杂,正常情况下的硬件实现不能达到高速信号处理的要求。在此,结合驰豫超前流水线技术和时序重构技术对算法进行优化改进,以便在对滤波性能没有很大影响的情况下能有效地切割关键路径,提高系统运行频率。
2.1 驰豫超前流水线优化
流水线技术是构造高速运行系统的一种实用技术。在硬件实现中,通过插入流水寄存器,可以斩断系统关键路径的长度,提高系统的运行频率。单向前馈割集表示能够斩断同向信号流,使系统成为完全不相连两个部分的分割形式。本文对于单向前馈割集路径插入一级流水寄存器,这里会使输出增加一个时钟滞后,但可以在不影响系统算法性能的情况下切割路径,提高系统频率。
驰豫技术也是一种可以构造实现流水线的方式,它通过近似的方式改变算法,在系统可以良好稳定运行的情况下得到适合流水实现的拓扑结构。对于GALJP算法,考虑到其中有多个环路迭代计算,无法使用前馈割集插入流水线的方式改进。对此,通过驰豫超前技术,提出的改进部分如下,对于格型预测器有:
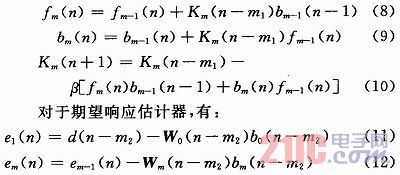
/2011.09/10/j.JPG)
式中:m=2,3,…,M+1,对于格型预测器,由于反射系数Km收敛迅速,所以在收敛后由于Km基本不变,故等式(8),式(9)是合理的。稳态性能则基本不变。
考虑收敛时段的式(10),令:
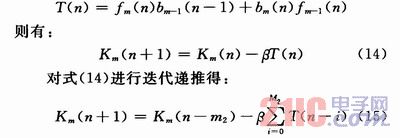
当系统处于收敛时段,恰当选取较小的β值时,式(15)的递推也是合理的,对比改变前的式(14),只是更新部分数值变大。这里可以看到,对于反射系数的驰豫,其算法收敛步长的区间将变得相对严格。类似的,对于期望响应估计器,对bm和Wm的驰豫变换在恰当选取稍小的μ的情况下也是合理的,同样的,会造成步长收敛区间变得相对狭窄。观察改进后的拓扑结构,对于期望响应估计器,改进后的误差更新和权系数更新可以同时流水进行,提高了模块速度,对于格型预测器,虽然改进方案没有使其能够流水线化,不能实质地提高系统频率,但是提供了驰豫寄存器,为后续优化做了准备。在这里,驰豫寄存器m1,m2的个数需要根据要求仔细选取。
2.2 时序重构优化
时序重构又称重定时,是一种在保持系统功能不变的前提下,改变系统的延迟数目和分布的方法。它在同步电路中有许多应用,如缩短系统时钟周期,减少系统寄存器数目,降低系统的功耗和逻辑综合的规模。对于时序不变系统,通过时序重构技术,可以在不改变算法功能的情况下,有效地切割关键路径,从而提高系统工作频率。时序重构的映射等式定义为:
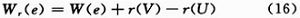
式中:Wr(e)表示重构映射后的路径e的延时;W(e)表示重构映射前的路径e的延时;r(V)表示路径e的前端处理单元V的重构参数;r(U)代表路径e的后端处理单元U的重构参数。通过合理地选取重构映射参数,可以得到合法的重构映射结构。
环路边界的定义为t1/wl,其中tl是环路l的运算时间;wl是环路l的延迟数目;迭代边界是环路结构的环路边界的最大值,定义为
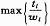
,迭代边界反映了一个反馈算法环路部分通过时序重构技术能达到的极限关键路径的大小。在此认为加法器和乘法器都是一个处理时间,考虑期望响应估计器模块的环路部分,如图2所示。
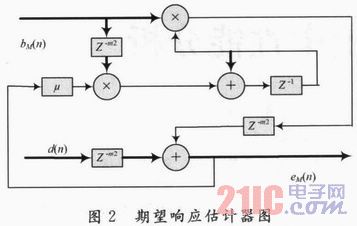
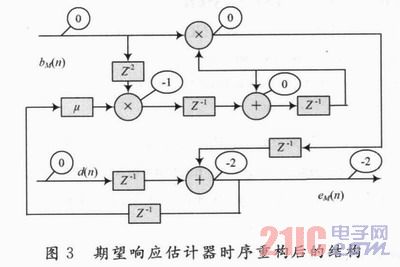
根据定义可以知道,迭代边界为4/(1+m2),使其迭代边界最小化,等于1,得到驰豫寄存器的数目m2=3。采用时序重构映射,根据式(16)得到重构后的算法结构,重构参数及重构结果如图3所示。
上一页 [1] [2] [3] 下一页