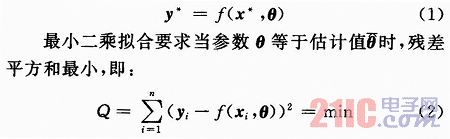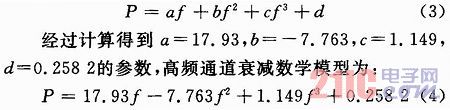2．2 高频信号传输通道功率衰减建模
    在测量数据处理中，常常遇到根据测量数据确定给定模型的参数；为离散测量数据建立连续模型2类问题。本文的数据处理工作属于第2种，在这类问题的测量数据处理方法中，比较好的是选取能够描述测量数据特征的某类曲线，在一定意义下从这类曲线中寻求一条“最好”的曲线作为实验数据对应的连续模型，并给出该连续模型对应的参数。这种处理思想被称为“拟合”，本文将采用经典的最小二乘拟合方法进行数据处理。
2．2．1 最小二乘拟合
    以两元模型为例，假设x和y分别为测量数据矢量，x*和y*分别为对应的真值矢量，f为拟合模型，θ为模型参数矢量，则：

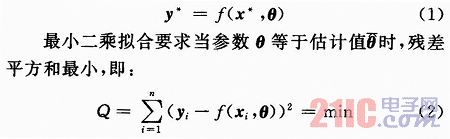
    由式(2)列出对应的正规方程并求解就可以得出模型参数的最小二乘估计值。最小二乘拟合的理论基础是高斯-马尔可夫定理，其发展已有约两百年的历史，在数据处理中被广泛应用。最小二乘估计具有无偏性和方差最小的性质，且与测量矢量所服从的概率分布无关，因而当测量矢量的概率分布形式不能严格知道，无法使用经典统计中的参数估计理论时，最小二乘拟合成为了数据处理的一种简便方法，同时这也是最小二乘拟合在数据处理中被广泛使用的原因。基于上述原因，本文选取最小二乘拟合方法对测试数据进行处理。
2．2．2 Matlab建立数学模型
    首先，以频率f=[0．03，0．1，0．5，1．0，1．5，2．0，2．5，2．7]，以及各频率点对应的功率衰减平均值p=[0．948，1．934，6．995，12．131，13．294，14．269，14．518，14．720]为数据点，画出二维空间的散点图，如图2所示。

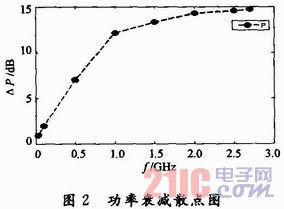
    根据其分布形状，选取三次多项式作为拟合曲线模型函数：

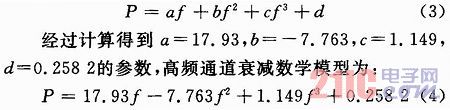
    具体实现步骤：
    (1)将f=[0．03，0．1，0．5，1．0，1．5，2．0，2．5，2．7]，p=[0．948，1．934，6．995，12．131，13．294，14．269，14．518，14．720]写入Matlab命令窗口；
    (2)输入命令函数cftool，回车弹出“Curve Fitting
Tool”窗口，如图3(a)所示；
    (3)点击按钮“Data”设置拟合数据分别为f，p，如图3(b)所示；

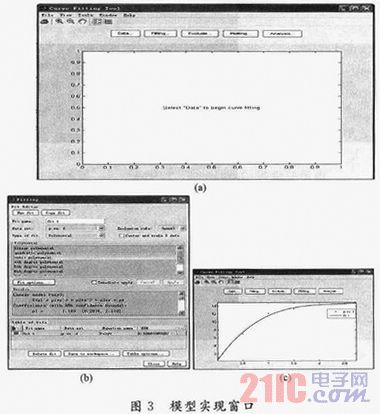
    (4)点击按钮“Fitting”，弹出窗口“Fitting”，选取拟合函数“cubIC polynomial”，点击“Apply”即可得到拟合数据模型，如图3(c)所示。

上一页  [1] [2] [3]  下一页