2 算法说明
2.1 失真距离量度
　　对一个MSVQ码本，为方便考虑假设共有2级码本。LSF参数为10维矢量。对LSF参数而言，其敏感矩阵(sensitivity matrix)是对角阵，因此可以用加权最小均方误差(WMSE)代替加权对数谱失真(WLSD)作为失真量度^[6]。量化失真
　　
　　r的经验值一般为0.15。
2.2 理论推导
　　对一个训练矢量集X和两级码本Y、Z，可以对X中每个矢量进行2级全搜索，得到最佳索引值对(i,j)。根据i和j的不同可以对X中每个矢量进行聚类。假设S为对第一级码字形成的聚类，S_i为所有X中第一级量化索引为i的训练矢量集合。同样假设R为第二级码字聚类,可知，{S₁,S₂，…，S_K1}和{R₁，R₂，…，R_K2}均是同一X集合的不同划分。对于X∈S_i，平均量化失真为：
　　
　　可以令v=E{x-U|x∈S_i}，则第三项为0。第二项恒为非负，所以
　　
　　通过多次迭代，可以得到联合优化的最优码本。
2.3 算法描述
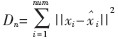
　　(1)设置初始码本，读入训练矢量文件，并对其进行两级码本全搜索，得到针对两级码本的聚类{S₁,S₂,…，S_K1}和{R₁，R₂，…，R_K2}。假设训练矢量个数为num，对所有训练矢量计算此时的量化失真之和，失真测度采用WLSD距离。设置迭代最大步数N，设置初始步数n=0；
　　(2)n=n+1，利用式(9)更新第一级码本；
　　(3)重新对训练矢量集进行全搜索，得到新的索引值对(i, j)，然后利用式(10)更新第二级码本；
　　(4)再次对训练矢量集进行量化搜索，得到新的索引值对(i, j)，并重新计算量化总畸变D_n；
　　(5)判断n=N？若n＜N，跳转至(2)继续进行迭代；若n=N，结束迭代，保存更新后的码字至码本文件。
2.4 算法的进一步优化
　　上述联合优化MSVQ算法中，很重要的一步就是对训练矢量进行聚类，使每个训练矢量得到一个最匹配的索引值对(i, j)。(i, j)应当是通过全搜索得到的全局最佳匹配矢量。在不需要在线更新码本的情况下，全搜索是可以采用的。然而如果在矢量维数较高时,想减小码本训练的运算量，也可以采用M进制序列搜索的方法。取M=8在实验中得到了很好的效果。这样即可得到一个性能近似的简化版JCO-MSVQ码本设计方法。

上一页  [1] [2] [3]