在多路实时语音处理系统中，基于高斯混合概率模型[1，2]的系统后端运算量非常大，采用log-add算法单元可以简化运算，提高运算效率。其函数形式为[3]：

   查表法可以认为是多项式次数为0的情况，随着精度要求的增加，查找表会变得很大[5]。函数逼近可以采用多项式拟合，首先根据所需要的精度确定多项式次数和分段的大小，然后计算每一段的多项式系数。
    设分段的大小为d(d=2-k，k=0，1，2…)，计算各段系数时，各段函数平移到区间[0，d），如图2所示。用Matlab进行多项式拟合依次得到各段系数。由此可以得出各段的拟合多项式为：

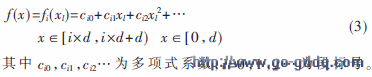
    这样实现时可以把二进制的定点数x分为MSBs和LSBs两段。MSBs对应段标号i，由段标号取出系数ci0，ci1，ci2…；LSBs对应浮点数xl，代表段内偏移值。由图3可以计算出f(x)。

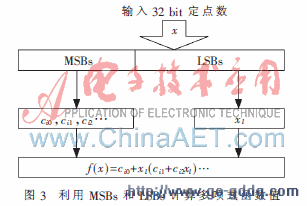
    MSBs和LSBs应该这样选取，例如定标为Q32.f，选择d=1/2，则MSBs为高32-（f-1）位，LSBs为低f-1位；选择d=1/4, 则MSBs为高32-(f-2)位，LSBs为低f-2位……；如果MSBs为32或31，则变成了查表法。
2 多项式拟合的实现方案
2.1 多项式次数与分段大小、精度的关系
    用Matlab进行仿真，表1列出了各种精度要求下各次多项式所需的分段大小(d)，其中?啄为精度要求，?茁为多项式的次数。
    由表1可以看出，相同次数的情况下，精度要求越高，分段大小d越小；而相同精度的情况下，次数越高，分段大小d越大。另外，次数越低，精度越高，分段大小d下降的数量级越快。

[1] [2] [3]  下一页