·上一文章：TMS320F28335与串行A/D转换器ADS7863的接口设计
·下一文章：超高频远距离无源射频接口电路设计方案
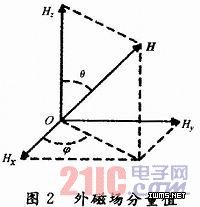
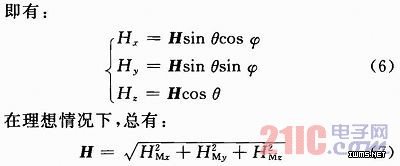
H为磁场总量，其大小在均匀外磁场中为一常数。式(7)表示坐标在原点，半径为H的标准球面，即三分量磁通门传感器输出的磁场总量为不变的常数。
考虑非正性交误差给三分量磁通门传感器带来的影响时，由式(1)和(6)可知，当传感器非正交时，只要传感器姿态变动，即角θ，φ发生变化。那么Hx，Hy，Hz的值也将发生变化，由于传感器实际测量坐标系的非正交，即α，β，γ的存在，HM必然会随之变化。因此，非正交性误差导致了传感器输出总量总是随传感器姿态的变化而变化。
实际的三分量磁通门传感器的输出与理想传感器输出相比，存在着误差。这些误差在传感器制成后就不再变化，即固有误差。从式(5)可知，只要求得α，β，γ，Sx，Sy，Sz，ex，ey，ez九个校正参数，就可以消除三分量磁通门传感器的误差。
那么校正传感器误差，就变成了求校正参数的问题：把不同姿态下，传感器输出的一系列传感器测量输出值HMk，(k=1，2，…，n)，作为参数α，β，γ，Sx，Sy，Sz，ex，ey，ez的函数；而外磁场值是恒定的，可以由实际的外磁场值H，或者根据传感器的测量值HMk平均值来逼
近外磁场的真实值H，即有：
进而，由式（5）作为校正公式，得到Hk。则可以表示校正参数的目标函数为：
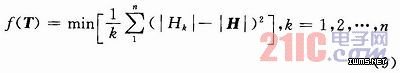
式中：T=(α，β，γ，Sx，Sy，Sz，ex，ey，ez)为校正参数向量。在传感器不同姿态下获得的输出值，通过式(5)换算得到校正值Hk。
当目标函数f(T)→0时，则有|Hk|→|H|。也就是校正值恒等于外磁场真实值，达到校正的目的，此时所得到的9个参数值即是所求校正参数。
3 使用遗传算法校正误差
校正传感器测量误差要同时求取9个校正参数α，β，γ，Sx，Sy，Sz，ex，ey，ez。为了较好地解决这些参数数量和单位不统一的情况下寻找最优解的问题，本文将遗传算法(GenetIC Algorithm)应用到校正参数的求取中，实现误差校正的全局最优化。
3．1 编码方式
实数编码是连续参数优化问题的自然描述，与二进制编码相比优点在于：提高解的精度和运算速度，避免了二进制编码带来的附加问题，如“Hamming悬崖”等。
由于9个校正参数数值大小和单位不同，选择实数编码方式可以将参数向量直接作为个体形式为：
式中：Xi=T，代表9个校正参数的个体。
3．2 适应度函数
适应度函数体现出优化对象与遗传算法的外部联系，算法与对象耦合的紧密程度决定了算法的稳定性和可靠性，应当在最大可能的情况下加强这种联系，这是提高遗传算法效率的最根本的途径。
由于求取优化校正参数的目标函数实际是求取函数最小值，且目标函数恒为正数，所以可以将目标函数直接转化为适应度函数：
式中：i=1，2，…，n。
3．3 精英保留策略
为保证每一代优良个体不被破坏，采用精英保留策略：如果下一代群体的最佳个体适应度值小于当前群体最佳个体适应值，则将当前群体最佳个体或者适应度值大于下一代最佳个体适应度值的多个个体直接复制到下一代，随机替代或替代最差的下一代群体中的相应数量个体。
精英保留策略保证了当前的最优个体不会被交叉、变异等遗传运算破坏，它是群体收敛到优化问题最优解的一种基本保障。
