摘要：静态磁场测量中，由于三分量磁通门传感器的非正交性，使得高分辨率测量要求不能得到满足，必须校正其测量误差。通过分析三分量磁通门传感器非正交性误差，给出其数学模型描述，提出了一种基于实数编码遗传算法的校正方法。应用于三分量磁通门传感器非正交性误差的校正，提高了传感器磁场测量的准确度。实验表明，该算法提高了三分量磁通门传感器非正交误差的校正效果。

关键词：三分量磁通门传感器；非正交性；误差校正；遗传算法

    引言
    静态地磁场是一个空间矢量场，即地磁场的值是一个既有大小也有方向的矢量值。准确地测量空间地磁场值或得到完整的地磁场信息，需要使用严格正交的三分量磁通门磁强计。通常进行地磁场测量时，往往把三分量磁通门传感器视为理想的三分量正交。但由于受加工工艺和安装工艺水平的限制，三分量磁通门传感器不可能做到绝对正交，这就给测量带来了不利影响。由于三分量磁通门传感器三轴向非正交，在某测点上当传感器运动时，其相对稳定的地磁场的标量输出并不是一个稳定的值，这就给地磁测量带来误差；由于三分量磁通门传感器三轴向非正交，致使按照理想情况进行计算的磁场标量值也产生了偏差。在分辨率要求较高的情况下，就必须考虑传感器非正交性带来的影响。
    在地磁场背景下，如果三分量磁通门传感器的正交误差大于0．5°，经过计算可知由三轴向非正交所带来的磁场测量误差将达数百纳特。文献中提出了一种基于共轭次梯度法的校正算法，并利用循环优化的思想对其进行了改进。文献中实现了基于扩展卡尔曼滤波和无迹卡尔曼滤波的两种算法并将其进行了比较。文献中将遗传算法应用于TWOSTEP算法，并比较了校正结果。本文提出使用一种基于实数编码遗传算法的校正算法，以提高误差校正的效果，提高磁强计的测量精度。

1 测量模型
    实际情况下，传感器的三个测量轴X1，Y1，Z1，由于技术水平的原因，并不是两两垂直的，所以基于传感器的测量坐标系并不是正交的。如图1所示，建立理想情况下的正交坐标系X，Y，Z，是两两绝对正交的。O-X1Y1Z1坐标系与O-XYZ之间的位置关系：Z轴与Z1轴重合；平面OX1Z1与平面OXZ共面，OX1与OX夹角为α；OY1轴与OXY平面的夹角为β，与OYZ平面的夹角为γ。

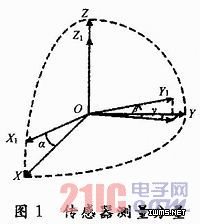
    HM与理想正交坐标系相对的磁场值H之间的关系可以用下面的公式表示：
   
    其中传感器实际测量值HM和外磁场理想正交分量值H分别为：
   

[1] [2] [3] [4]  下一页