在新的图像压缩标准JPEG2000中，采用9/7、5/3提升小波变换作为编码算法，其中5/3小波变换是一种可逆的整数变换，可以实现无损或有损的图像压缩。在通用的DSP芯片上实现该算法具有很好的可扩展性、可升级性与易维护性。用这种方式灵活性强，完全能满足各种处理需求。

　　1 提升算法

　　提升算法[1]是由SwELDens等在Mallat算法的基础上提出的，也称为第二代小波变换。与Mallat算法相比，提升算法不依赖傅立叶变换，降低了计算量和复杂度，运行效率相应提高。由于具有整数变换及耗费存储单元少的特点，提升算法很适合于在定点DSP上实现。

　　小波提升算法的基本思想是通过基本小波逐步构建出一个具有更加良好性质的新小波。其实现步骤为分解(split)、预测(preDICt)和更新(update)。

　　首先按照对原信号进行对称延拓得到新的x(n)。

　　分解是将数据分为偶数序列x(2n)和奇数序列x(2n+1)二个部分；

　　预测是用分解的偶数序列预测奇数序列，得到的预测误差为变换的高频分量：H(n)=x(2n+1)-{[x(2n)+x(2n+2)]>>1}

　　更新是由预测误差更新偶数序列，得到变换的低频分量： L(n)=x(2n)+{[H(n)+H(n-1)+2]>>2}

　　计算过程如图1所示。

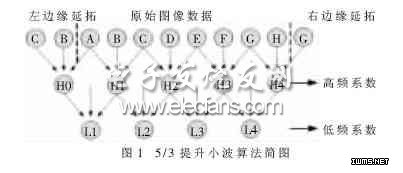
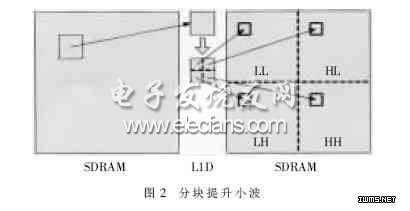
在这种方法中，SDRAM中的一个数据块首先传输到L2中，然后取到L1D中进行水平方向的提升，再对该块进行垂直方向的提升。这样，由于垂直提升所需的数据都在L1D中，避免了此处数据缓存缺失的产生，使总的缺失数大大降低。
2.3 数据传输
(1)SDRAM与L2间的数据传输
由于EDMA[6][7]数据传输与CPU运行相互独立，因此在L2中开辟两块缓存：EDMA在CPU处理InBuffA的同时将下一块数据传输到InBuffB，解决了CPU读取低速设备SDRAM引起的时延，如图3所示。

边界延拓主要是用于计算高频系数。分析发现，水平提升时，当前数据块每一行的最后一个高频系数与下一个块在该行的第一个高频系数相同。所以只要把当前块的这些系数保存起来，在对下一块进行水平提升时第一个高频系数就不需要再进行计算，因此也就不需要再对其左边界进行延拓了。垂直方向的提升也是同样的道理。在程序中添加两个数组，分别用于存放当前块的每一行与每一列的最后一个高频系数。采用这种方法就可以降低程序的复杂度，提高执行效率，减少缺失的发生。
像素扩展函数pix_pand[9]是采用TI的IMGLIB算法库。水平提升与垂直提升函数均由作者用线性汇编语言编写，充分利用64x系列DSP的半字处理指令，采用半字打包技术，最大限度地提高程序的执行效率。
水平提升时，将每行的数据重新排序，变成如图5所示的结构。

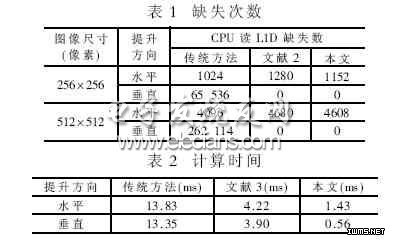
表2列出了几种方法的计算性能。由于本文采用了多种优化技术，运算速度提高了4～10倍。试验证明这些方法十分有效。