摘要：正交频分复用(OFDM)技术作为一种高速信息传输技术，具有频谱利用率高、抗频率选择性衰落和码间干扰能力强等优势，但由于OFDM信号是通过多载波调制后的合成信号，所以OFDM信号存在较高的峰均比，这会给传输系统带来许多不利因素，限制了OFDM技术的应用。文章针对OFDM系统中存在的高峰均比提出了一些相关的抑制技术，提高了系统的可靠性和有效性。在实际应用中，可根据要求和需要选择适合的方法。
关键词：正交频分复用；峰均比；编码技术

    1 OFDM系统中峰均比的定义
    一个OFDM符号是由多个独立的经过调制的子载波信号相加而成，在某个时刻，若多个子载波以同一个方向进行累加时，就会产生比较高的峰均功率比(Peak-to-Average Power Ratio,PAPR)，简称峰均比。对于包含N个子信道的OFDM系统来说，当N个子信号都以相同的相位求和时，所得到的信号的峰值功率就会是平均功率的N倍。如图1所示，在这个例子里，峰均功率是平均功率的16倍，其中所有子载波都受到相同数据符号的调制。

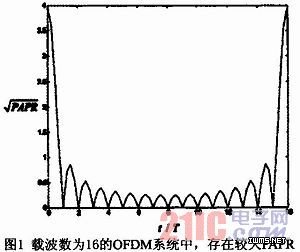
    我们定义峰均比为OFDM的峰值功率和其平均功率之比，即：
   
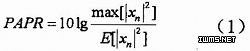
    其中，xn表示在OFDM系统中经过IFFT变换以后得到的输出信号。基带信号的峰均比可以表示为PART=10lgN，当N=256时，PAPR=24dB，当然这只是一个极端情况，OFDM系统内的峰均比通常不会达到这一数值。
    我们还用峰值系数(crest factor)来描述信号的峰值变化，该参数定义为最大信号值与方均根值之比：
   

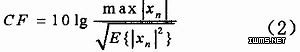
2 峰均比的性能衡量——CCDF函数
    对于包含N个子载波的OFDM系统来说，其中经过IFT计算得到的功率归一化的复基带信号是：
   
    其中，Xk表示第k个子载波上的调制符号。对于OPSK来说，xk∈{1，-1，j，-j}。根据中心极限定理可知，只要子载波个数N足够大，就可以判断x(t)的实部和虚部都将遵循高斯分布，其均值为零，方差为0．5(实部和虚部各占整个信号功率的一半)。因此，可以得知，OFDM符号的幅值r服从瑞利分布，而其功率分布则要服从两个自由度的中心耽分布，其中，均值为零，方差为1，由于自由度为二的中心x2，分布的概率密度函数为ppower(y)=e-y，因此，可以计算得到其累积分布函数(CDF，Cumulative Distribution Function)为：
   
    当然，也可以从另一个角度来衡量OFDM系统的PAPR分布，即计算峰均比超过某一个门限Z的概率，得到互补累计分布函数CCDF：
   
    图2是不同N数条件下，CCDF的理论曲线图。从图中可以看出，在给定PAPR门限值的条件下，N越大，出现高于门限值的概率也越大。

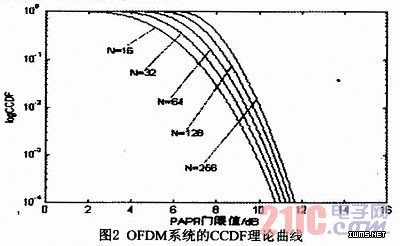
    在随后的讨论中，一般都采用CCDF来衡量OFDM系统内的PAPR分布。

[1] [2] [3] [4]  下一页