3．2 扰码技术
    这类技术的基本思想并不是要降低信号幅度的最大值，而是降低峰值出现的概率。它是通过对原OFDM符号作线形分割和线形交换，以减少信号峰值出现的概率，优化子信道的载波相位以寻找能得到最低PAPR的相位组合。一般的模式是在发送端对每一个OFDM符号，根据某些规则产生多个候选的时域波形，并计算每一波形的PAPR，最终传输PAPR最小的那一个。这种方法虽然并不能保证所有传输信号的幅度都小于门限值，但是却大大降低了峰值出现的概率，也就降低了限幅噪声对系统带来的不利影响。它在结构上容易实现，应用灵活，是目前最具应用潜力也是最为热门的方案。这里主要介绍选择性映射(SLM)和部分传输序列方法(PTS)两种方法。
3．2．1 选择性映射
    OFDM系统发射机内的信号可以表示为：xk=IFFT[Xn]，(n,k=0，…，N-1)。假设存在M个不同的、长度为N的随机相位序列矢量(Pμ=p0(μ)，…，pN-1μ)，其中(μ=0，…，M-1)，pi(μ)=exp(jφi(μ))，φi(μ)在[0，2π]之内均匀分布。可以利用这朋个相位矢量分别与IFFT的输入序列x进行点乘，则可以得到M个不同的输出序列X(μ)间，即：
   
    其中(·)表示向量之间的点乘。然后对所得到的M个序列X(μ)分别实施IFFT计算，相应得到M个不同的输出序列X(μ)=(X0(μ)，…，XN-1(μ))。最后在给定PAPR门限值的条件下，从这个M个时域信号序列内选择PAPR性能最好的用于传输。
    SLM方法的原理框图如图5所示。

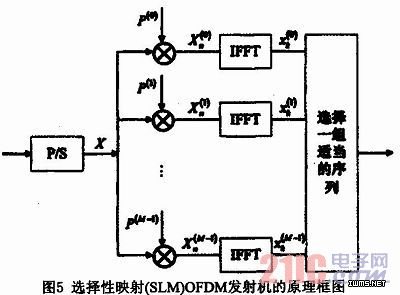
    设峰均比的门限值为PAPR0，则原始OFDM序列的PAPR超过门限值的概率定义为Pr{PAPR>PAPR0}；而这M个序列x(μ)，(μ=0，…，M-1)的PAPR都超过门限值的概率就会变为[PT{PAPR>PAPR0}]M，根据式(5)可以计算出SLM-OFDM系统内PAPR的CCDF为：
   
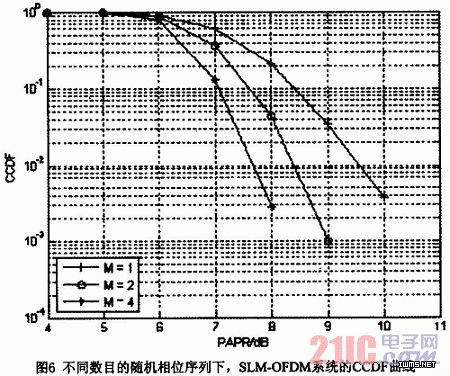
    其中M=1时，就是原始OFDM系统PAPR分布的CCDF。图6表示了子载波数为128时，不同肘取值下，OFDM系统采用SLM算法PAPR的CCDF曲线。
这种算法的缺点是需要额外计算M-1组的IFFT运算，且接收机必须知道选择的相位。

上一页  [1] [2] [3] [4]  下一页