星载计算机系统中电子器件容易受到空间环境电磁场的辐射和重粒子的冲击，从而导致器件运行出错，特别是存储器中数据容易出现错误，需要具有检纠错功能的电路模块对其进行纠正，以免造成严重的后果。基于汉明码的纠错原理.根据对64位数据进行检纠错处理的需要，设计一个利用8位校验码，以实现该功能的算法逻辑，并通过FPGA实现。经过仿真验证，该模块具备检测2位错误，纠正1位错误的功能，而且也能较好地满足实时性的要求，具有一定的实际应用意义。

　　引 言

　　随着现代技术的发展，作为现代高科技代表的航天工程，对星载计算机的依赖程度也越来越高。由于宇宙中存在着大量的带电粒子，星载计算机硬件系统的电子器件会受到电磁场的辐射和重粒子的冲击，其相互作用产生各种效应，其中单粒子反转(SEU)效应的影响尤为明显，它将引起卫星工作的异常或故障。这种错误若不及时进行纠正，将会影响计算机系统的运行和关键数据的正确性，造成程序运行不稳定和设备状态改变。

　　1 纠错原理

　　汉明码(Hamming Code)是由RIChard Hamming于1950年提出的，属于线性分组码的范畴，其基本原理是将信息码元与监督码元通过线性方程式联系起来的，每一个监督位被编在传输码字的特定比特位置上。系统对于错误的数位无论是原有信息位中的，还是附加监督位中的都能把它分离出来。(n，k)线性分组码的生成矩阵G和校验矩阵H分别为n×k和n×(n-k)维矩阵，其中校验矩阵H决定信息位与校验位的关系，在编码和译码中都要用到。线性码的最小码距为d，即校验矩阵H中任意d-1列线性无关，它与码的纠错能力有以下关系：

　　(1)检测P个随机错误，要求d≥e+1;

　　(2)纠t个随机错误，要求d≥2t+1;

　　(3)纠t个随机错误，同时检测e(e≥t+1)个随机错误，要求d≥e+t+1。

　　作为一种典型的线性分组码，标准汉明码的码长n=2m-1，监督位数为m，信息位数为k=n-m，最小码距d=3，因此它的纠错能力t=1，是一种常用纠单个位错误的编码方式。还可以根据需要对标准汉明码进行扩展，增加1个校验位对所有位进行监测，就得到扩展汉明码。1个(n，k)汉明码经过扩展以后，就变成了(n+1，k)汉明码。扩展以后的汉明码d=4，t=2，e=1，可以纠正单个位错误，并检测出双位的错误。对64位的数据进行纠错设计，满足信息位数大于64要求的最短的标准汉明码为n=26-1时的(127，120)码，它具有7个监督校验位。根据汉明码信息位删减后其纠错能力较之前不会降低的特性，将该码的信息位缩短为64位，使用了(71，64)的删减汉明码。这里设计了一种7个校验位同64个信息位的对应计算关系如图1所示。

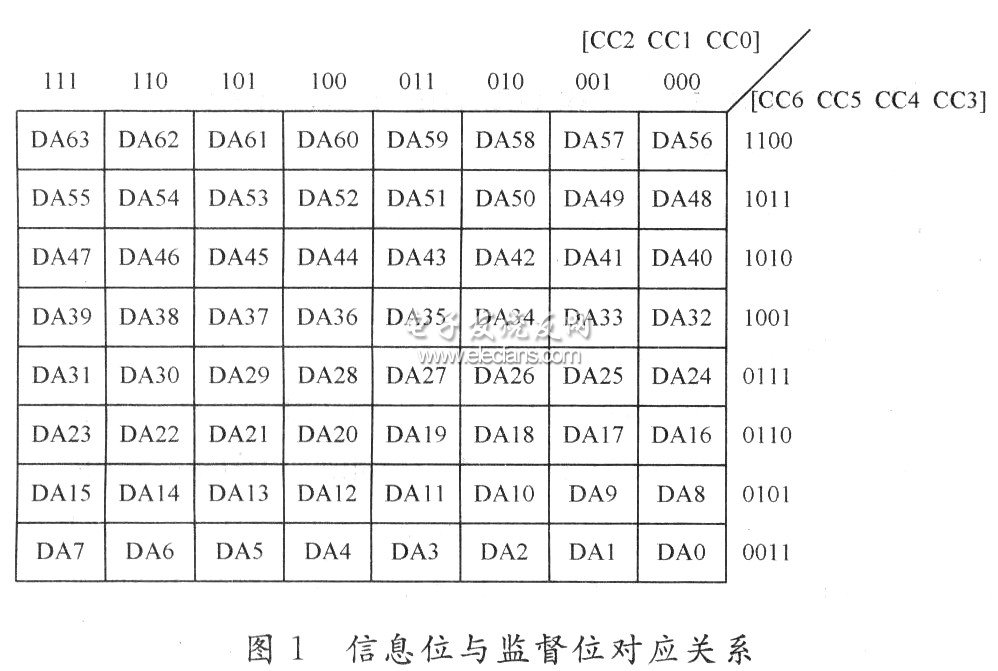
　　图1中DA0～DA63为信息位;CC0～CC6为监督校验位。其中CCO是所有位于编号末位数为1列中信息位数据的奇偶校验计算结果。与之类似，CCl对应于所有位于编号次低位数为1列中的信息位。同理，CC3～CC6分别对应了行号各位数为1行中的信息位数据。通过这个对应关系表，可以得出整个汉明码的生成公式：

　　M=DG

　　式中：M为生成的(71，64)汉明码矩阵，每个行向量是一组汉明码;D为信息位数据矩阵行，64个信息位组成一个行向量;G成为汉明码生成矩阵，可以根据上述的对应计算关系得出来。

[1] [2] [3]  下一页